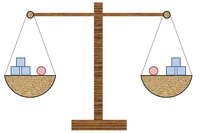
Allgemeines
Beispiel:
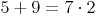
Dies ist eine Gleichung, da ein =Zeichen zwei Rechnungen in Beziehung stellt.
Probe:
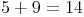
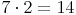
Gleichungen können neben Zahlen und Rechenzeichen auch noch Variable (also Buchstaben bzw. in der Grundschule noch Platzhalter).
Beispiele:
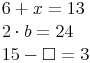
Diese Variablen müssen nun durch Zahlen ersetzt werden. Dazu wählt man Zahlen aus einer sogenannten Grundmenge G aus, in unseren Beispielen immer (falls nicht anders angegeben) aus der Menge der natürlichen Zahlen.
Das Lösen der Gleichung bedeutet nun also, aus einer Grundmenge jene Zahlen in die Gleichung einzusetzen, um eine richtige Gleichung zu erhalten.
Die Menge aller Zahlen, die zur richtigen Lösung der Gleichung führen, wird als Lösungsmenge L bezeichnet.
Beispiel:
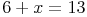
Diese einfache Gleichung kann man im Kopf lösen: 
Daher gilt auch: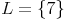
Gleichungen trennen zwei Terme durch ein =Zeichen voneinander. Sie bestehen aus Zahlen, Rechenzeichen und Variablen.
Für die Variablen darf man aus einer vorgegebenen Menge an Zahlen wählen, der sogenannten Grundmenge G.
Alle Zahlen, die man anstatt der Variablen einsetzen kann und die beim Einsetzen eine richtige Gleichung ergeben, bilden die Lösungsmenge L.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar