Bruchgleichungen
Kommt bei einer Gleichung die Variable (z.B. x) mindestens einmal im Nenner vor, so spricht man von einer Bruchgleichung.
Ein Beispiel einer solchen Bruchgleichung ist der nebenstehenden Abbildung zu entnehmen.
In diesem Kapitel möchten wir eine Anleitung geben, wie Bruchgleichungen gelöst werden können.
Beispiel:
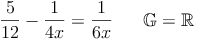
1. Definitionsmenge
Die Definitionsmenge schließt alle Zahlen aus, die einen Nenner zu Null machen würden:
4x = 0 / : 4
x = 0
6x = 0 / : 6
x = 0
Somit gilt: Die Definitionsmenge unserer Bruchgleichung sind alle reellen Zahlen außer der Zahl 0!
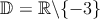
2. Gemeinsamer Nenner:
Um eine Bruchgleichung lösen zu können, müssen die Brüche auf den gleichen Nenner gebracht werden.
Erstelle dir dazu eine Tabelle. Plane für jeden Nenner eine Zeile ein und eine weitere für den gemeinsamen Nenner. Schreibe nun jeweils jeden Faktor in eine eigene Spalte - gleiche Zahlen bzw. Variablen untereinander.
Der gemeinsame Nenner ergibt sich nun als allen Faktoren der einzelnen Spalten:
| 12 = 2 . 2 . 3 | 2 | 2 | 3 | |
| 4x = 2 . 2 . x | 2 | 2 | x | |
| 6x = 2 . 3 . x | 2 | 3 | x | |
| Gemeinsamer Nenner | 2 | 2 | 3 | x |
Der gemeinsame Nenner lautet also 
3. Lösen der Bruchgleichung
Sieh dir nun den gemeinsamen Nenner an und vergleiche ihn mit den einzelnen Nennern. Die Bruchterme müssen nun mit den fehlenden Faktoren multipliziert werden:
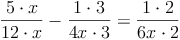
Nun multiplizieren wir mit dem gemeinsamen Nenner - welcher dadurch wegfällt: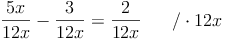
Die Gleichung ohne Brüche wird nun durch Äquivalenzumformungen gelöst: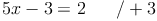


Die Zahl 1 ist in der Definitionsmenge enthalten, somit kommt sie auch in die Lösungemenge: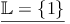
4. Probe:
Wir setzen das Ergebnis (in unserem Fall die Zahl 1) sowohl in die linke als auch in die rechte Seite der Gleichung ein. Sind beide Ergebnisse identisch, so haben wir die Bruchgleichung richtig gelöst.
Linke Seite: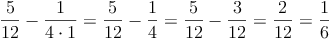
Rechte Seite: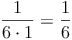
Kontrolle: 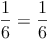
1. Definitionsmenge bestimmen: Schließe alle Zahlen aus, die einen Nenner zu Null machen würden!
2. Gemeinsamer Nenner: Erstelle dir zur Ermittlung eine Tabelle!
3. Brüche gleichnamig machen: Multipliziere die einzelnen Brüche mit den fehlenden Faktoren!
4. Gleichung bruchfrei machen: Multipliziere mit dem gemeinsamen Nenner!
5. Gleichung lösen: Löse die brichfreie Gleichung durch Äquivalenzumformungen!
6. Kontrolle der Lösung: Überprüfe, ob die Lösungszahl in der Definitionsmenge enthalten ist!
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
