Lösen von Gleichungen mit Brüchen

In diesem Kapitel möchten wir Ihnen zeigen, wie Sie Gleichungen mit Brüchen lösen können, wenn die Variable im Zähler steht.

Lösen von Gleichungen mit Brüchen

In diesem Kapitel möchten wir Ihnen zeigen, wie Sie Gleichungen mit Brüchen lösen können, wenn die Variable im Zähler steht.

Beispiel:



\frac{4x}{3} - \frac{x}{2} = 5

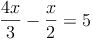
Damit man eine Gleichung mit Brüchen lösen kann, müssen die Brüche auf einen gleichen Nenner gebracht werden. Der kleinste gemeinsame Nenner von 3 und 2 ist 6. Somit muss der erste Bruch mit 2 und der zweite Bruch mit 3 erweitert werden:

\frac{8x}{6} - \frac{3x}{6} = 5 \qquad / \cdot 6

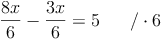
Da nun alle Brüche den gleichen Nenner haben, kann man diese Brüche auflösen, indem man mit dem gemeinsamen Nenner mutlipliziert:

8x - 3x = 30

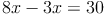
Die Gleichung kann nun gelöst werden: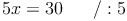

5x = 30 \qquad / : 5

\underline{x = 6}

Probe:

Wir setzen nun die Lösung x = 6 in die Angabe ein: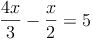

\frac{4x}{3} - \frac{x}{2} = 5

\frac{4 \cdot 6}{3} - \frac{6}{2} = 5

\frac{24}{3} - \frac{6}{2} = 5

8 - 3 = 5

5 = 5 \qquad w.A.

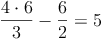
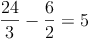
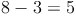
Lösen von Gleichungen mit Brüchen

1. Alle Brüche auf einen gemeinsamen Nenner bringen!

2. Die gesamte Gleichung mit dem gemeinsamen Nenner multiplizieren!

3. Gleichung durch Äquivalenzumformungen weiter lösen!

Kommentar verfassen