Natürliche Zahlen im Stellenwertsystem darstellen
Es gibt eine Menge unterschiedlicher Stellenwertsysteme (z.B. Binärsystem, Hexadezimalsystem, ...). In unserem alltäglichen Gebrauch arbeiten wir mit dem Zehnersystem (Dezimalsystem).
Beispiel:
Vor uns liegen eine Menge an Murmeln, die wir nun zählen sollen.
Dazu ordnen wir sie zuerst und bilden Zehner-Gruppen.
Es geht sich genau aus, dass wir 3 Gruppen zu jeweils 10 Murmeln bilden können.
Insgesamt liegen also 30 Murmeln vor uns.
Die 30 einzelnen Murmeln (30 E) haben wir zu 3 Gruppen zu je zehn Murmeln zusammengefasst (3 Z).
In der Mathematik schreiben wir:
30 E = 3 Z
Zehnersystem:
Unser Stellenwertsystem (Zehnersystem) besteht aus 10 Ziffern:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Zahlen, die größer als 9 setzen sich aus mehreren Ziffern zusammen.
z.B. 30 = 3Z 0E (drei Zehner, null Einer)
z.B.: 512 = 5H 1Z 2E (5 Hunderter, 1 Zehner, 2 Einer)
Stellenwerttabelle:
Eine Stellenwerttabelle (auch Stellenwerttafel) hilft uns bei der Einordnung von Zahlen.
Folgende Stellenwerte gibt es:
Einer (E), Zehner (Z), Hunderter (H), Tausender (T), Zehntausender (ZT), Hunderttausender (HT), Millionen (M), Zehnmillionen (ZM), Hundertmillionen (HM), Milliarden (Md), Zehnmilliarden (ZMd), Hundertmilliarden (HMd), Billionen (B), ...
Jede natürliche Zahl lässt sich durch die Ziffern 0, 1, 2, 3, 4, 5, 6, 7, 8 und 9 im Zehnersystem darstellen.
Zahlen, die größer als 9 sind werden zur nächstgrößeren dekadischen Einheit (Einer, Zehner, Hunderter, ...) zusammengefasst.
Jede Zahl besteht aus Ziffernwerten (0 bis 9) und Stellenwerten (E, Z, H, ...).
Beispiel: 716
Ziffernwerte: 7, 1, 6
Stellenwerte: 7H, 1Z, 6E
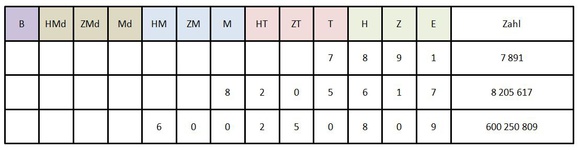
Beispiele:
7 891 = 7T 8H 9Z 1E
8 205 617 = 8M 2HT 5T 6H 1Z 7E
600 250 809 = 6HM 2HT 5ZT 8H 9E
Beachte: Nullwerte (z.B. 0Z) müssen nicht angeschrieben werden!
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar