Die Basis eines gleichschenkligen Dreiecks mit Hilfe des pythagoräischen Lehrsatzes berechnen
Beispiel:
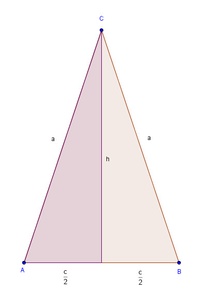
Von einem gleichschenkligen Dreieck kennt man die Länge des Schenkels a = 9,5 cm und die Länge der Höhe h = 9 cm. Berechnen Sie die Länge der Basis c!
Zeichnet man die Höhe ein, so teilt diese das gleichschenklige Dreieck in zwei gleich große rechtwinkelige Dreiecke.
In einem rechtwinkeligen Dreieck gilt der Lehrsatz des Pythagoras, daher gilt: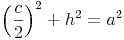
Wir formen um: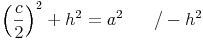
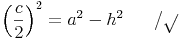
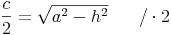
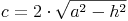
Beispiel (Forts.):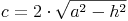
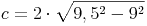
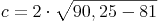
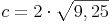
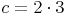
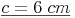
Antwort: Die Länge der Basis c des gleichschenkligen Dreiecks beträgt ca. 6 cm.
Die Basis eines gleichschenkligen Dreiecks berechnen:
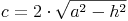
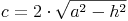
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar