Die Schenkellänge eines gleichschenkligen Dreiecks mit Hilfe des pythagoräischen Lehrsatzes berechnen
Beispiel:
Von einem gleichschenkligen Dreieck kennt man die Länge der Basis c = 6 cm und die Länge der Höhe h = 9 cm. Berechnen Sie die Länge des Schenkels a!
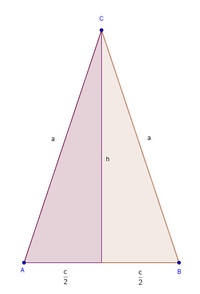
Zeichnet man die Höhe ein, so teilt diese das gleichschenklige Dreieck in zwei gleich große rechtwinkelige Dreiecke.
In einem rechtwinkeligen Dreieck gilt der Lehrsatz des Pythagoras, daher gilt: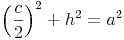
Wir formen um: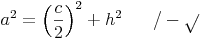
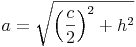
Beispiel (Forts.):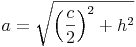
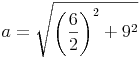
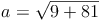
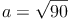
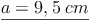
Antwort: Die Länge des Schenkels a des gleichschenkligen Dreiecks beträgt ca. 9,5 cm.
Den Schenkel a eines gleichschenkligen Dreiecks berechnen:
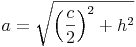
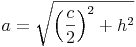
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
ebers
Ich habe eine dreickscheibe
Unten 1694 senkrecht 748
Wie lang ist die schräge
Mika Immecke
Ich verstehe es trotzdem nicht
Ledda
Danke. Schon das mit dem in zwei Teilen hat mir gereicht. (Hätte ich eigentlich auch selbst drauf kommen können)
Linda
Wie würde man den Schenkel a mit dem Flächeninhalt und der Höhe c berechnen?
Edgard Schmidt
Ich habe von einem gleichseitigen Dreieck nur die Höhe. Wie kann ich die Fläche berechnen?