Beweise für den Lehrsatz des Pythagoras
Beweise für den Lehrsatz wurden erst von Pythagoras' Schülern gefunden. Mittlerweile kennen wir weit über 300 unterschiedliche Beweise. Anhand des bekanntesten Beweises leiten wir Ihnen den Lehrsatz her.
Der Lehrsatz des Pythagoras gilt nur für rechtwinklige Dreiecke.
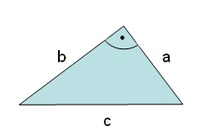
1) Wir konstruieren ein beliebiges rechtwinkliges Dreieck:
a = 3 cm , b = 4 cm , c = 5 cm
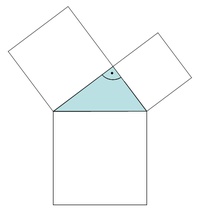
2) Wir konstruieren über jede Dreiecksseite ein Quadrat
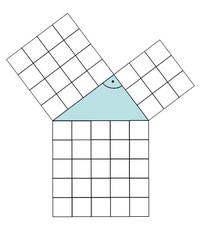
3) Wir zeichnen in den 3 Quadraten 1x1cm-Quadrate (=Quadratzentimeter) ein, um den Flächeninhalt einfacher ablesen zu können.
4) Berechnung der Flächeninhalte:
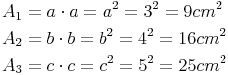
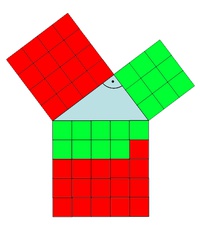
5) Vergleich der Flächeninhalte:
Wir erkennen. dass die beiden Quadrate über die Seiten a und b zusammen genauso groß sind wie das Quadrat über c:
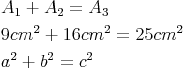
Die Summe der Flächeninhalte der Kathetenquadrate (= Quadrate über den kürzeren Dreiecksseiten) ist gleich dem Flächeninhalt des Hypotenusenquadrates (= Quadrat über der längsten Dreiecksseite).
In einem rechtwinkligen Dreieck mit den Seiten a, b und c gilt deshalb: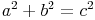
In einem rechtwinkligen Dreieck mit den Seiten a, b und c gilt deshalb:
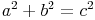
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Heinz Weber
Ihr Beweis für den Satz des Pythagors setzt im ersten Schritt voraus, dass ein Dreieck mit den Seitenlängen 3, 4 und 5 einen rechten Winkel enthält...