Der Inkreis eines regelmäßigen Sechsecks
Zu jedem regelmäßigen Vieleck lässt sich ein Inkreis zeichen.
Um den Inkreismittelpunkt zu erhalten, zeichen wir die drei Diagonalen AD, BE und CF ein.
Um den Inkreisradius zu erhalten, halbieren wir eine beliebige Seite des regelmäßigen Vielecks und verbinden diesen Punkt mit dem Mittelpunkt.
Da man nun den Radius erhalten hat, kann man nun auch den Inkreis konstruieren.
Der Inkreisradius entspricht der Höhe eines der gleichseitigen Dreiecke. Daher gilt die Formel zur Berechnung der Höhe eines gleichseitigen Dreiecks auch für die Berechnung des Inkreisradius:
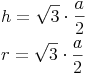
Der Inkreis eines regelmäßigen Sechsecks
Zu jedem regelmäßigen Sechseck lässt sich ein Inkreis zeichnen.
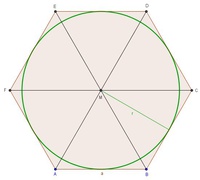
Der Inkreismittelpunkt ist der Schnitpunkt der Diagonalen, der Inkreisradius ist die kürzeste Verbindung des Inkreismittelpunktes mit dem Mittelpunkt einer Seite des regelmäßigen Sechsecks.
Inkreisradius:
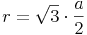
Zu jedem regelmäßigen Sechseck lässt sich ein Inkreis zeichnen.
Der Inkreismittelpunkt ist der Schnitpunkt der Diagonalen, der Inkreisradius ist die kürzeste Verbindung des Inkreismittelpunktes mit dem Mittelpunkt einer Seite des regelmäßigen Sechsecks.
Inkreisradius:
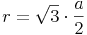
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Jens
Der Innenkreis wird in der Technik auch Schlüsselweite genannt, wenn man z.B. mit einem Schraubenschlüssel eine Sechskannt-Schraube anzieht