Flächeninhalt

Herleitung der Formel zur Berechnung des Flächeninhalts eines Trapezes

Der Flächeninhalt des Trapezes

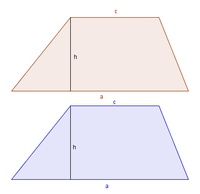
Herleitung der Flächeninhaltsformel:

1) Wir konstruieren zwei beliebige gleich große Trapeze.

2) Nun wird die Höhe auf die Seite a eingezeichnet.

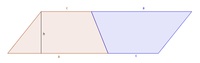
3) Das 1. Trapez bleibt liegen, das 2. Trapez wird so"umgelegt", dass die beiden Schenkel b übereinander liegen.

4) Ein Parallelogramm ist entstanden, dessen Fläche noch immer so groß ist wie jene der beiden ursprünglichen Trapeze zusammen.

5) Berechnung der Fläche des Parallelogramms:

${A{_P}=Seite{\cdot}Höhe$

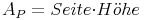
Die Seite des Parallelogramms entspricht der Summe der Seiten a und c, die Höhe h ist identisch:

Seite: a+c

Höhe: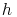

Setzt man dies in die Flächeninhaltsformel des Parallelogramms ein, so ergibt sich:

${A{_P}=(a+c){\cdot}h$

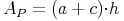
Die Fläche eines Trapezes ist halb so groß wie jene des Parallelogramms:

Flächeninhalt des Trapezes:

${A=\frac{(a+c){\cdot}h}{2}$

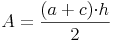
Flächeninhalt = [(Seite a + Seite c) x Höhe h] / 2

Kommentar #39492 von Paul Deisenhammer 22.04.17 11:58 Paul Deisenhammer: bei einem gleichschenkligen bzw. bei einem allgemeinem trapez, wie reche ich mr da die diagonale e bzw. f aus?

mfg
paul
Kommentar #41068 von Jafari 01.05.18 08:45 Jafari: Wie kann man die seite a und die höhe Wissen vom Flächen Inhalt
Kommentar #47627 von Niemand 15.12.22 10:56 Niemand: Wer hat gefragt? (Lösung=Name)