Winkel

Die Winkel im Trapez

In einem Trapez beträgt die Winkelsumme so wie in jedem anderen Viereck 360°.

In einem Trapez verlaufen zwei gegenüberliegende Seiten parallel zueinander. Deshalb beträgt die Summe der beiden Winkel, die an einem Schenkel (= nicht parallele Seite) anliegen, immer 180°.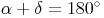
$\alpha + \delta = 180^\circ$
$\beta + \gamma = 180^\circ$

Begründung:

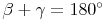
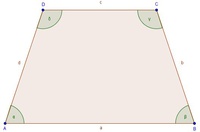
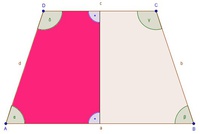
Wir zeichen an beliebieger Stelle eine Normale auf die Seite a bzw. die Seite c. Dadurch entstehen zwei neue Vierecke, deren Winkelsumme wiederum jeweils 360° beträgt.

Wir konzentrieren uns auf das linke der beiden neuen Vierecke:

Alle Vier Winkel müssen 360° betragen, zwei Winkel davon sind rechte Winkel (90°), also:

$360^\circ - 90^\circ - 90^\circ = 180^\circ$

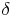Es bleiben also 180° für die beiden Winkel $\alpha$ und $\delta$ übrig.

Analog könnte man natürlich nun auch im rechten neuen Viereck vorgehen.

Winkelberechnung in einem Trapez

Beispiel:

geg.: Trapez: 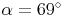$\alpha = 69^\circ$ , $\beta = 72^\circ$

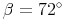
Berechnen Sie die Größen der beiden anderen Winkel!

Gamma berechnen:

$\begin{align} & \beta + \gamma = 180^\circ \\ & 72^\circ + \gamma = 180^\circ \qquad / - 72^\circ \\ & \gamma = 180^\circ - 72^\circ \\ & \gamma = 108^\circ \\ \end{align}$

Delta berechnen:

$\begin{align} & \alpha+ \delta= 180^\circ \\ & 69^\circ + \delta = 180^\circ \qquad / - 69^\circ \\ & \delta = 180^\circ - 69^\circ \\ & \delta = 111^\circ \\ \end{align}$

Die Winkel in einem Trapez:

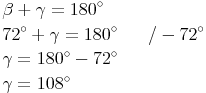
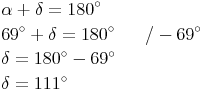
In einem Trapez beträgt die Winkelsumme so wie in jedem anderen Viereck 360°.

Außerdem gilt auch noch:
$\alpha + \delta= 180^\circ$
$\beta + \gamma = 180^\circ$

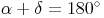
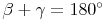
Dieser Artikel hat mir geholfen. das half mir
... leider nicht ... leider nicht
Kommentar Kommentar
2,9
187 Bewertungen

Kommentar #591 von dodri 02.06.12 23:19 dodri: oben ist ein fehler, da steht beta + gamma = 360 es müsste wie ganz unten auf der seite beta + gamma = 180 heißen
Kommentar #593 von Admin 06.06.12 20:02 Admin: Hallo!
Vielen Dank! der Fehler wurde bereichts behoben!
Kommentar #8406 von Mehl 14.01.14 16:51 Mehl: Danke hat mir sehr geholfen für die kommende arbeit. :D
Kommentar #10726 von YOLOz 20.10.15 18:39 YOLOz: Ich wollte eigentlich wissen wie man die seite e berechnet (und das bitte möglichst unkompliziert).
Danke für eure hilfe!
:D
Kommentar #14270 von Maxi 09.04.16 15:06 Maxi: Gilt das mit den 180 Grad nur für ein paralleles Trapez?
Kommentar #32110 von ronaldo 07.01.17 19:36 ronaldo: das hat mir überhaupt nicht geholfen :(
Kommentar #35702 von Gabi 02.02.17 18:41 Gabi: Super Artikel, aber wie bereits von dodri erwähnt: Oben steht immer noch:
Beta + Gamma = 360
Kommentar #35704 von Roland Lammel 02.02.17 18:51 Roland Lammel: Danke für den (erneuten) Hinweis, ist ausgebessert!
Kommentar #40196 von unbekannt 03.10.17 16:23 unbekannt: wie berechnet man die 3 Winkel, wenn man nur einen Wert hat?
Kommentar #40916 von Charterflieger 25.03.18 20:11 Charterflieger: Wie berechne ich Die Winkel alpha und gamma wenn keiner der beiden gegeben ist?
Kommentar #41740 von Sarah 29.10.18 18:59 Sarah: Wenn winkel a 48° hat welche winkelgrösse hat dann ß ???
Kommentar #41784 von Momed 06.11.18 20:08 Momed: Berechnen von innenwinkel eines Trapezes Steht in meiner aufgabe aber ich kann das nicht rechnen
Wir müssen mit sin cos und tan arbeiten aber ich kann das nicht könnte mir jemand helfen
Kommentar #43132 von Sophia 12.11.19 18:14 Sophia: Bei mir ist nur Gamma gegeben, wie berechnet ich da die anderen Winkel?
Kommentar #43134 von H 12.11.19 18:25 H: wie rechnet man alpha aus wenn kein anderer Winkel gegeben ist ????

Winkel

Die Winkel im Trapez

Winkelberechnung in einem Trapez

Kommentar verfassen

Ähnliche Arbeitsblätter