Berechnung des Radius des Kegels, wenn die Oberfläche und die Mantellinie bekannt sind
Beispiel
Ein Kegel hat eine Oberfläche von 175,9 cm² und eine Mantellinie von 10 cm.
Herleitung der Formel
Aus dem Kapitel wissen wir bereits, dass sich die Oberfläche des Kegels aus der Summe von Grundfläche (Kreis) und Mantelfläche (Kreisausschnitt) errechnet.
Daraus ergibt sich folgende Formel:
Wiederholung: Oberfläche des Kegels:
Die Oberfläche eines Kegels setzt sich aus der Grundfläche und der Mantelfläche zusammen:
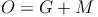
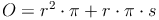
Die Oberfläche eines Kegels setzt sich aus der Grundfläche und der Mantelfläche zusammen:
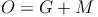
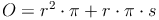
Nachdem wir allerdings die Oberfläche und die Mantellinie des Kegels kennen, nicht aber den Radius, müssen wir die Formel so umformen, dass r (der Radius) alleine auf einer Seite steht:
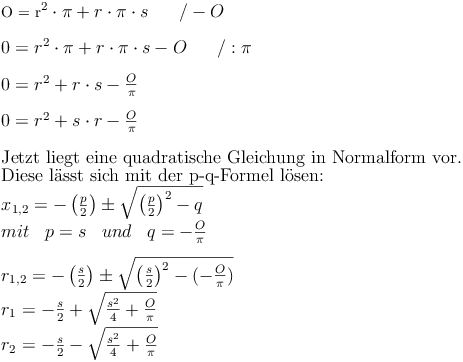
Beispiel (Fortsetzung)
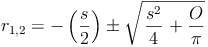
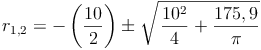
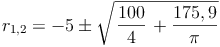
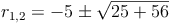
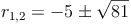
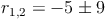
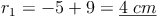
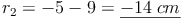
Da der Radius keine negative Zahl sein kann, ist 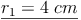 die Lösung dieses Beispiels.
die Lösung dieses Beispiels.
Probe: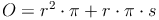
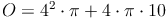
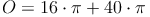
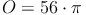
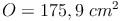
Antwort:
Der Zylinder hat einen Radius von 4 cm.
Berechnung des Radius eines Kegels, wenn Oberfläche und Mantellinie bekannt sind:
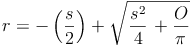
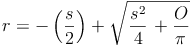
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar