Das Volumen einer Hohlkugel
In diesem Kapitel möchten wir Ihnen zeigen, wie man das Volumen einer Hohlkugel berechnen kann.
Eine Hohlkugel wird in unserem Sprachgebrauch manchmal auch als Kugelschale bezeichnet.
Unter einer Hohlkugel versteht man eine Kugel, die eine bestimmte "Wandstärke" hat und in der Mitte hohl ist.
Mathematisch handelt es sich dabei um zwei konzentrische Kugeln (also mit gleichem Mittelpunkt) mit unterschiedlichen Radien.
Je mehr sich die beiden Radien unterscheiden, desto größer is auch die Wandstärke dieser Hohlkugel.
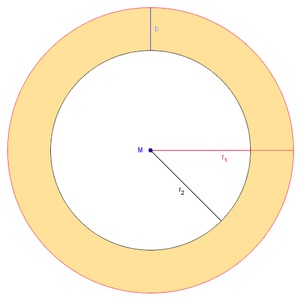
Die ebene Querschnittsfläche einer solchen Hohlkugel ist ein Kreisring.
Um eine Formel zur Berechnung des Volumens einer Hohlkugel herleiten zu können, brauchen wir die Formel zur Berechnung des Volumens einer Kugel, die wir bereits im vorhergehenden Kapitel "Das Volumen einer Kugel" hergeleitet haben:
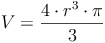
Herleitung der Formel:
Eine Hohlkugel besteht also aus zwei konzentrischen Kugeln mit unterschiedlichen Radien.
Somit kommt man zum Volumen der Hohlkugel, indem man zuerst das Volumen der größeren Kugel mit dem Radius r1 berechnet und anschließend das Volumen der kleineren Kugel (= Hohlraum) mit dem Radius r2 abzieht (subtrahiert). Übrig bleibt das Volumen der Hohlkugel.
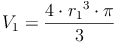
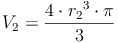

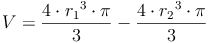
Beispiel:
Berechnen Sie das Volumen einer Hohlkugel mit einem Außendurchmesser von 12 cm und einem Innendurchmesser von 10 cm.
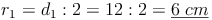
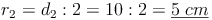
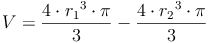
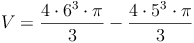
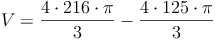
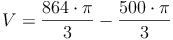
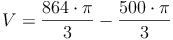
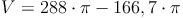
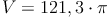

- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Sabine
Ich finde die Seite echt toll und hilfreich. Vielen Dank