Das Volumen der Kugel
Unter dem Volumen (oder auch Rauminhalt) eines Körpers versteht man den räumlichen Inhalt dieses Körpers.
Umgangssprachlich würde man sagen: all jenes, das in diese Kugel hineinpasst (Flüssigkeit, ...)
Das Volumen wird mit V abgekürzt und entspricht in der ebenen Geometrie dem Flächeninhalt.
Herleitung der Formel:
Für die Herleitung der Volumsformel einer Kugel arbeiten wir mit Umfüllen.
Dazu teilen wir eine Kugel in 2 gleich große Halbkugeln.
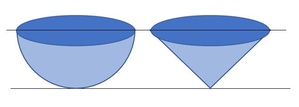
Nun vergleichen wir das Volumen einer Halbkugel mit dem Volumen eines Kegels. Dazu müssen folgende Eigenschaften gegeben sein:
Halbkugel und Kegel haben denselben Radius und dieselbe Höhe.
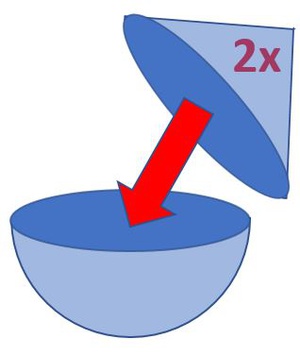
Nun füllen wir den Kegel mit Flüssigkeit und schütten diese in die Halbkugel. Wir können erkennen, dass dies genau 2 Mal möglich ist.
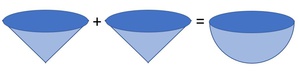
Es gilt: Das Volumen eines Kegels passt genau 2 Mal in eine Halbkugel mit gleichem Radius und gleicher Höhe!
Möchte man nun beide Halbkugeln (die ganze Kugel) befüllen, so muss man mit dem Kegel insgesamt 4 Mal umschütten.
In einem anderen Kapitel haben wir bereits die Formel zur Berechnung des Volumens eines Kegels hergeleitet:
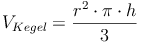
Das Volumen der Kugel ist 4 Mal so groß wie das Volumen des Kegels, Radius u. Höhe sind gleich: r = h
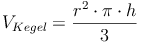
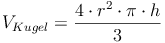
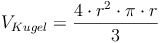
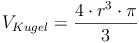
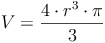
Beispiel:
geg.: Kugel: r = 5 cm
ges.: V
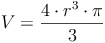
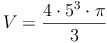
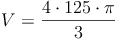
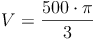
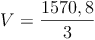
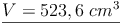
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Stefan Feuchtinger
Das ist doch keine mathematische Herleitung, hier wird das Ergebnis als Startpunkt verwendet. Das ist bestenfalls ein physikalisches Experiment welches eine naeherungweise Gleichheit vermuten laesst. Austria: zero points!