Das Volumen der Kugel - Umkehraufgaben
Von einer Umkehraufgabe sprechen wir, wenn das Volumen der Kugel gegeben und der Radius bzw. der Durchmesser zu berechnen ist.
Man muss nun die Volumenformel so umformen, dass man sich die fehlende Größe (den Radius r bzw. den Durchmesser d) berechnen kann.
Beispiel:
Eine Kugel hat ein Volumen von 113,1 cm³. Berechne den Radius bzw. den Durchmesser dieser Kugel!
Herleitung der Formeln
Aus dem Kapitel wissen wir bereits, dass das Volumen der Kugel 4 Mal so groß ist wie das Volumen eines Kegels mit gleichem Radius und gleicher Höhe: r = h.
Daraus ergeben sich folgende Formeln:
Das Volumen der Kugel ist 4 Mal so groß wie das Volumen eines Kegels mit gleichem Radius und gleicher Oberfläche.
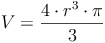
Nachdem wir allerdings das Volumen der Kugel kennen, nicht aber den Radius, müssen wir die Formel so umformen, dass r (der Radius) alleine auf einer Seite steht:
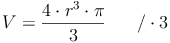
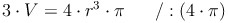
![\frac{3 \cdot V}{4 \cdot \pi} = r^3\qquad / \sqrt[3]{ } \frac{3 \cdot V}{4 \cdot \pi} = r^3\qquad / \sqrt[3]{ }](/media/formulas/eece839c87e75c96727fd8dbbbc9f25c.png)
![\sqrt[3]{\frac{3 \cdot V}{4 \cdot \pi}} = r \sqrt[3]{\frac{3 \cdot V}{4 \cdot \pi}} = r](/media/formulas/1eba2b4de57d5f6f840c60c96537dfa2.png)
Beispiel (Fortsetzung)
![r = \sqrt[3]{\frac{3 \cdot V}{4 \cdot \pi}} r = \sqrt[3]{\frac{3 \cdot V}{4 \cdot \pi}}](/media/formulas/1ab23d77e8446a96fbb14e4f46e75b0f.png)
![r = \sqrt[3]{\frac{3 \cdot 113,1}{4 \cdot \pi}} r = \sqrt[3]{\frac{3 \cdot 113,1}{4 \cdot \pi}}](/media/formulas/80b621c4e6e3b7ffcb2f5c8c5969f131.png)
![r = \sqrt[3]{\frac{339,3}{4 \cdot \pi}} r = \sqrt[3]{\frac{339,3}{4 \cdot \pi}}](/media/formulas/722952f72406bfda1aa3ca952acab225.png)
![r = \sqrt[3]{\frac{339,3}{12,57}} r = \sqrt[3]{\frac{339,3}{12,57}}](/media/formulas/7ba1848944739cea8de47fc033a58724.png)
![r = \sqrt[3]{27} r = \sqrt[3]{27}](/media/formulas/708f9ede79169ca9f40a01503e44e13b.png)
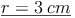
Antwort:
Die Kugel hat einen Radius von 3 cm bzw. einen Durchmesser von 6 cm.
![r = \sqrt[3]{\frac{3 \cdot V}{4 \cdot \pi}} r = \sqrt[3]{\frac{3 \cdot V}{4 \cdot \pi}}](/media/formulas/1ab23d77e8446a96fbb14e4f46e75b0f.png)
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar