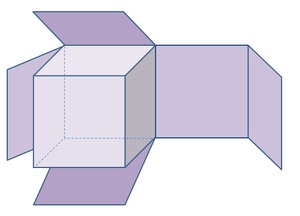
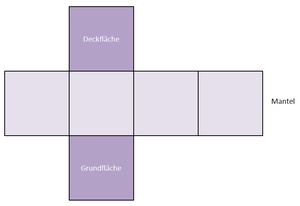
Umkehraufgaben zur Oberflächenberechnung beim Würfel
Beispiel:
Ein Würfel hat eine Oberfläche von 294cm².
Berechnen Sie die Kantenlänge s dieses Würfels!
Herleitung der Formel:
Aus dem vorherigen Kapitel wissen wir bereits, dass die Oberfläche eines Würfels die Summe aller sechs Flächen (= Quadraten) ist:
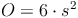
Nachdem wir allerdings die Oberfläche, nicht aber die Kantenlänge kennen, müssen wir die Formel so umformen, dass s (die Kantenlänge) alleine auf einer Seite steht.
Schritt 1: Das Gegenteil des Multiplizierens ist das Dividieren, also muss beim Umformen durch 6 dividiert werden:
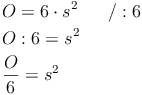
Schritt 2: Das Gegenteil des Quadrierens ist das Quadratwurzelziehen, also muss beim Umformen die Quadratwurzel gezogen werden.
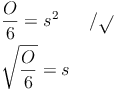
Beispiel (Forts.)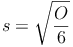
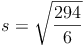
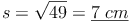
Probe: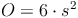
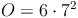
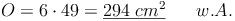
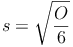
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar