Volumen - Umkehraufgaben

Hier finden Sie eine Formel, wie Sie die Seitenlänge s eines Würfels berechnen können, wenn das Volumen V bekannt ist.

Umkehraufgaben zur Volumsberechnung beim Würfel

Beispiel:

Ein Würfel hat ein Volumen von 3 375 cm³. Berechnen Sie die Seitenlänge des Würfels!

Herleitung der Formel:
Aus dem vorherigen Kapitel wissen wir bereits, dass sich das Volumen eines Würfels aus dem Produkt von Länge, Breite und Höhe errechnet:

Volumen des Würfels:

V = s \cdot s \cdot s = s^3

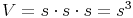
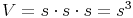
Nachdem wir allerdings das Volumen, nicht aber die Seitenlänge kennen, müssen wir die Formel so umformen, dass s (die Seitenlänge) alleine auf einer Seite steht.

Um die 3. Potenz wegzubekommen, müssen wir das Gegenteil davon machen, nämlich die 3. Wurzel ziehen - natürlich auf beiden Seiten:

\begin{align} & V = s^3\qquad / \sqrt[3]{} \\ & \sqrt[3]{V} = s \\ \end{align}

Beispiel (Forts.):

\begin{align} & s = \sqrt[3]{V} \\ & s = \sqrt[3]{3 375} \\ & s = \underline{15\ cm} \\ \end{align}

Probe:

\begin{align} & V = s^3 \\ & V = s \cdot s \cdot s \\ & V = 15 \cdot 15 \cdot 15 \\ & V = 3 375\ cm^3 \\ \end{align}

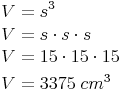
Antwort:

Der Würfel hat eine Seitenlänge von 15 cm.

Berechnung der Seitenlänge eines Würfels, wenn das Volumen bekannt ist:

s = \sqrt[3]{V}

Seitenlänge = Kubikwurzel aus dem Volumen

Kommentar verfassen