Die Oberfläche des Würfels
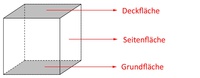
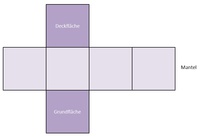
Im Kapitel Seitenflächen des Würfels haben wir bereits erläutert, dass die Grundfläche, die Deckfläche und die 4 Seitenflächen, die den Mantel bilden, alle gleich groß sind.
Diese 6 gleich großen Flächen bilden also die Oberfläche des Würfels.
Um die Oberfläche zu berechnen, berechnen wir zuerst einmal den Flächeninhalt einer Seitenfläche.
Da die Seitenfläche ein Quadrat ist, brauchen wir die Formal zur Berechnung des Flächeninhalts eines Quadrates:
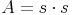
Da die Oberfläche des Würfels aus 6 gleich großen Quadraten besteht, muss man zur Gesamtberechnung den Flächeninhalt einer Seitenfläche mal 6 rechnen:
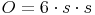
Beispiel:
geg.: Würfel: s = 7 cm
ges.: O
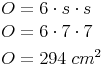
Oberfläche des Würfels:
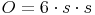
Die Oberfläche eines Würfels besteht aus 6 gleich großen Quadraten.
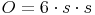
Die Oberfläche eines Würfels besteht aus 6 gleich großen Quadraten.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar