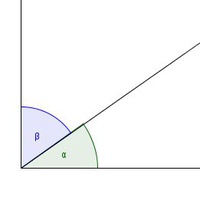
Komplementärwinkel
Beispiel:
Konstruieren Sie den Winkel 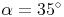 .
.
a) Konstruieren Sie den komplementären Winkel 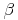 zum Winkel
zum Winkel  .
.
b) Berechnen Sie den komplementären Winkel 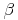 zum Winkel
zum Winkel  .
.
c) Stellen Sie eine Formel auf, die den Zusammenhang zwischen dem Winkel  und seinem komplementären Winkel
und seinem komplementären Winkel 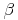 beschreibt.
beschreibt.
Wir konstruieren zuerst den Winkel 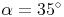 .
.
Anschließend konstruieren wir einen rechten Winkel, dessen Scheitel identisch mit dem Winkel  ist und bei dem einer der beiden Winkelschenkel identisch sind.
ist und bei dem einer der beiden Winkelschenkel identisch sind.
Jenen Winkel, der vom zweiten Schenkel des Winkels  und dem zweiten Schenkel des rechten Winkels eingeschlossen wird, bezeichnen wir als Winkel
und dem zweiten Schenkel des rechten Winkels eingeschlossen wird, bezeichnen wir als Winkel 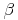 .
.
Die beiden Winkel ergänzen einander auf 90° und sind deshalb komplementär.
c)
Die beiden Winkel  und
und 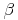 ergänzen einander auf 90°. Mathematisch geschrieben sieht das folgendermaßen aus:
ergänzen einander auf 90°. Mathematisch geschrieben sieht das folgendermaßen aus:
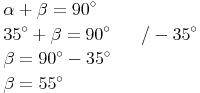
Komplementärwinkel (Komplementwinkel) sind Winkel, die einander auf 90° ergänzen.
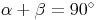
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar