Nebenwinkel
Wir konstruieren zwei beliebige Geraden, die einander in einem Punkt schneiden. Nun bezeichnen wir einen der vier dadurch entstandenen Winkel als Winkel  .
.
Jene beiden Winkel, die neben diesem Winkel  liegen, werden als Nebenwinkel bezeichnet. Wir benennen Sie in unserem Beispiel mit den Namen
liegen, werden als Nebenwinkel bezeichnet. Wir benennen Sie in unserem Beispiel mit den Namen 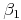 und
und 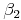 .
.
Zwei Winkel, die zusammen 180° ergeben, werden als Supplementwinkel, als Supplementärwinkel oder als Ergänzungswinkel bezeichnet.
In unserem Beispiel können wir erkennen, dass der Winkel und sein Nebenwinkel zusammen jeweils 180° ergeben:
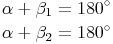
Nebenwinkel sind also supplementär (= ergänzen einander auf 180°).
Beispiel:
Berechnen Sie die Größe der Nebenwinkel, wenn der Winkel 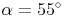
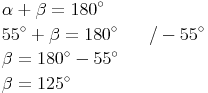
Nebenwinkel:
Nebenwinkel sind supplementär (= sie ergänzen einander auf 180°).
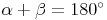
Nebenwinkel sind supplementär (= sie ergänzen einander auf 180°).
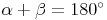
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
amelie
danke! hat mir sehr weitergeholfen!
beni
Cool
Lisa
Ihr habt mir super weitergeholfen!!