Potenzmenge
Jede nicht leere Menge M besitzt immer zwei Teilmengen:
- die leere Menge {}
- die Menge M selbst
Also gilt:
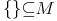 und
und 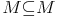
Es gibt jedoch noch weitere Teilmengen. Alle Teilmengen fasst die Potenzmenge zusammen:
Potenzmenge Definition
Unter der Potenzmenge P(M) versteht man die Menge aller möglichen Teilmengen von M.
Potenzmenge Beispiele
Beispiel 1: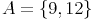
Die Potenzmenge von A lautet somit:
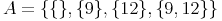
Beispiel 2: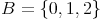
Die Potenzmenge von B lautet somit:
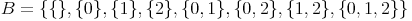
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Anonym
Sehr übersichtlich und strukturiert. Einfach erklärt mit guten Beispielen! Super!
nixe
ganz einfach erklärt. sehr gut
Hristo
Interessant, aber welche sind die Elemten z.Bsp hier - P(P(P(P(die leere Menge)))) ?