3. Binomische Formel

Die 3. Binomische Formel

Herleitung - 1. Möglichkeit:

$(a + b) \cdot (a - b) =$
$= aa - ab + ba - bb =$
$= a^2 - ab + ab - b^2 =$
$= a^2 - b^2$

Herleitung - 2. Möglichkeit:

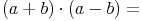
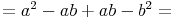
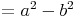
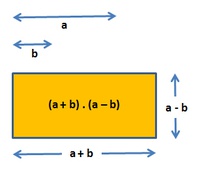
Wir berechnen den Flächeninhalt des orangen Rechtecks auf 2 verschiedene Arten. Dazu nehmen wir folgende Seitenlängen an: a = 6 cm , b = 1,5 cm

$A_{Quadrat} = s^2$

$A_{Rechteck} = l \cdot b$

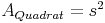
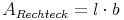
Möglichkeit I:
Wir erhalten die Länge des orangen Rechtecks, wenn wir zu der Länge a die Länge b dazurechnen. Die Breite erhalten wir, wenn wir von der Länge a, die Länge b abziehen. Nun berechnen wir den Flächeninhalt:

$A = (a + b) \cdot (a - b) =$
$= (6 + 1,5) \cdot 6 - 1,5) =$
$= 7,5 \cdot 1,5 =$
$= 33,75 cm^2$

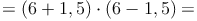
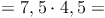
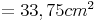
Möglichkeit II
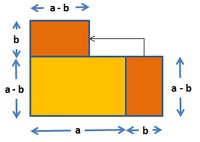
Wir schneiden von unserem Rechteck ein kleineres Rechteck, welches b lang, is ab. Dieses abgeschnittene Rechteck legen wir um 90° gedreht oben auf das Rechteck drauf.

Entstanden ist nun eine Fläche, die fast ein Quadrat ist.

Von der Länge des Rechtecks (a + b) wird b ageschnitten:
(a + b) - b = a +b - b = a
Zur Breite des Rechtecks (a - b) wird b dazugegeben :
(a - b) + b = a - b + b = a

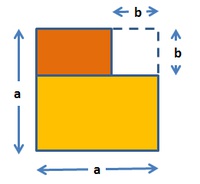
Es entsteht also ein Quadrat mit der Seitenlänge a, aus dem ein kleineres Quadrat mit der Seitenlänge b herausgeschnitten wurde.
Wir berechnen den Flächeninhalt also folgendermaßen:
$A = a^2 - b^2 = 6^2 - 1,5^2 = 36 - 2,25 = 33,75 cm^2$

Zusammenfassung:

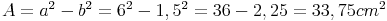
Da bei beiden Möglichkeiten dasselbe Ergebnis herauskommt, kann man die beiden Rechenwege gleichsetzen: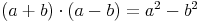
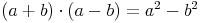
$(a + b) \cdot (a - b) = a^2 - b^2$

3. Binomische Formel:

$(a + b) \cdot (a - b) = a^2 - b^2$

Beispiel:

$(8m + 3n) \cdot (8m - 3n) = 64m^2 - 9n^2$

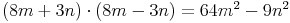
Dieser Artikel hat mir geholfendas half mir
Dieser Artikel hat mir nicht geholfen... leider nicht
Kommentar zu dieser Seite abgebenKommentar
Frage im Forum stellenForum
Offizielle Facebook-SeiteFacebook

Kommentar schreiben

Kommentare zu diesem Thema