Binomische Formeln hoch 3
Auf dieser Seite möchten wir veranschaulichen, wie man Binomische Formeln mit dem Exponenten (der Hochzahl) 3 lösen kann. Mathematisch geschrieben sieht die Ausgangssituation folgendermaßen aus:

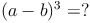
Herleitung (a + b)³
Zur Herleitung der Formel schreiben wir die Ausgangssituation als Produkt von Summen auf. Dann lösen wir diese Terme.
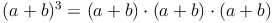
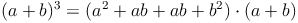
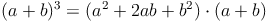
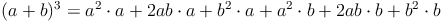

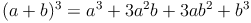
Beispiel (a + b)³
Zur Kontrolle, ob unsere soeben hergeleitete Formel auch stimmt, setzen wir für die Variablen a und b beliebige Zahlen (z.B. 4 und 5) ein.
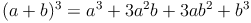
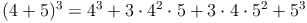
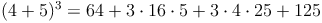

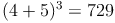
Probe: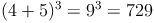
Herleitung (a - b)³
Zur Herleitung der Formel schreiben wir die Ausgangssituation als Produkt von Differenzen auf. Dann lösen wir diese Terme.
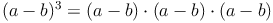
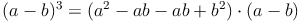
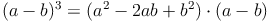

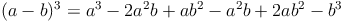
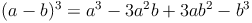
Beispiel (a - b)³
Zur Kontrolle, ob unsere soeben hergeleitete Formel auch stimmt, setzen wir für die Variablen a und b beliebige Zahlen (z.B. 5 und 3) ein.
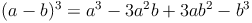
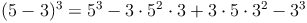
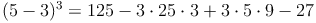
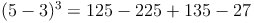

Probe:
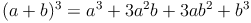
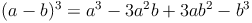
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar