Multiplizieren von Summen und Differenzen: Formelsammlung
Hier finden Sie nochmals alle Formeln zu diesem Thema! Die Beweise bzw. Herleitungen der einzelnen Formeln finden Sie auf den vorhergehenden Seiten.
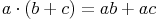
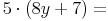
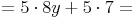
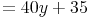
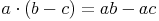
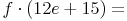
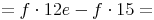
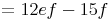
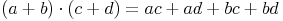
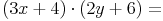
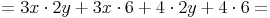
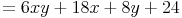
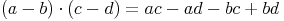
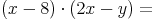
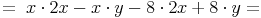
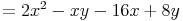
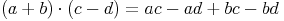
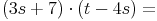
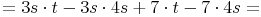

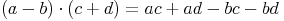
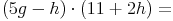
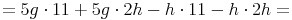
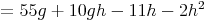
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar