Multiplizieren von Differenzen I: Ein Faktor ist ein eingliedriger Ausdruck
Beispiel:
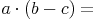
Wir wollen die Fläche des kleineren Rechtecks von der Fläche des größeren Rechtecks abziehen:
Möglichkeit 1:Wir berechnen zuerst den Flächeninhalt der des größeren Rechtecks, dann des kleineren Rechtecks und subtrahieren die beiden Ergebnisse:
A = Länge mal Breite
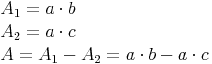
Wir legen die beiden Flächen übereinander und versuchen nun den Flächeninhalt der übriggebliebenen lila Fläche zu berechnen:
A = Länge mal Breite
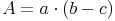
Beide Berechnungen führen zum selben Ergebnis, deshalb kann man die beiden Ergebnisse gleichsetzen:
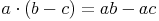
Multiplikation von Differenzen, wenn ein Faktor eingliedrig ist:
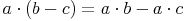
Beispiel: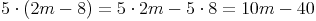
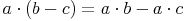
Beispiel:
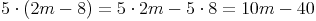
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
