Ähnlichkeiten beim gleichschenkligen Dreieck

Gleichschenklige Dreiecke sind grundsätzlich nicht ähnlich.

Ähnlichkeiten beim gleichschenkligen Dreieck

Erfahren Sie mehr über das gleichschenklige Dreieck
Beispiel:

Konstruieren Sie ein gleichschenkliges Dreieck mit den Seitenlängen 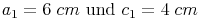a_1 = 6\ cm \text{ und } c_1 = 4\ cm sowie anschließend ein zweites gleichschenkliges Dreieck mit den Seitenlängen a_2 = 4\ cm \text{ und } c_2 = 6\ cm!

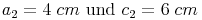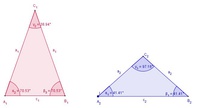
Winkel:

Vergleicht man die Winkel des 1. Dreieckes mit den Winkeln des 2. Dreieckes, so sieht man, dass diese nicht identisch sind:

\alpha_1 \not = \alpha_2

\beta_1 \not = \beta_2

\gamma_1 \not = \gamma_2

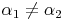
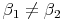
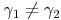
Da die zugehörigen Winkel nicht gleich groß sind, sind die beiden Dreiecke auch nicht ähnlich!

\triangle A_1B_1C_1 \thicksim \triangle A_2B_2C_2


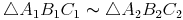
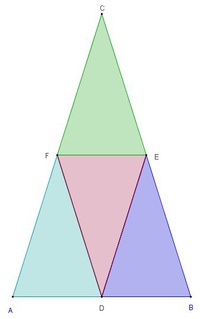
Verbindungsstrecken der Seitenmittelpunkte:

Halbiert man alle 3 Seiten und verbindet die dadurch entstandenen Punkte D, E und F miteinander, so ergeben sich 4 gleich große (kongruente) Dreiecke, die dem Ausgangsdreieck ähnlich sind.

\triangle ABC \thicksim \triangle ADF \thicksim \triangle BDE \thicksim \triangle DEF \thicksim \triangle CEF

Ähnlichkeiten beim gleichschenkligen Dreieck:

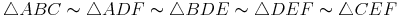
Gleichschenklige Dreiecke sind grundsätzlich nicht ähnlich!

\triangle A_1B_1C_1 \not \thicksim \triangle A_2B_2C_2

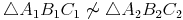
Halbiert man allerdings die Seiten und verbindet die Halbierungspunkte miteinander, so entstehen 4 kongruente Dreicke, die dem Ausgangsdreieck öhnlich sind!

Kommentar verfassen