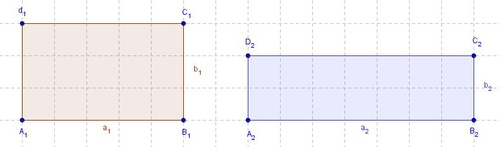
Ähnlichkeiten beim Rechteck
BeispielWir wollen herausfinden, ob beliebige Rechtecke immer ähnlich zueinander sind. Dazu konstruieren wir folgende Rechtecke:
Rechteck 1: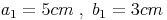
Rechteck 2: 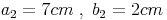
Dazu vergleichen wir die Winkel und Seiten der beiden Rechtecke miteinander.
Winkel:
Ähnlichkeit:
Entsprechende Winkel ähnlicher Figuren sind gleich groß.
( ,
, 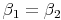 ,
, 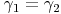 , ...)
, ...)
Entsprechende Winkel ähnlicher Figuren sind gleich groß.
(
 ,
, 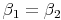 ,
, 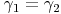 , ...)
, ...)
Da in einem Rechteck jeder Winkel ein rechter Winkel ist (90°), stimmt diese Behauptung bei unseren beiden Rechtecken!
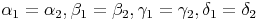
Seiten:
Ähnlichkeit:
Entsprechende Seiten ähnlicher Figuren sind proportional zueinander (haben das gleiche Verhältnis).
(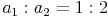 ,
, 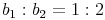 ,
, 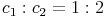 , ...)
, ...)
Entsprechende Seiten ähnlicher Figuren sind proportional zueinander (haben das gleiche Verhältnis).
(
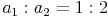 ,
, 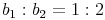 ,
, 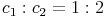 , ...)
, ...)
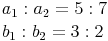
Die beiden Verhältnisse sind nicht identisch, daher sind die beiden Rechtecke auch nicht ähnlich!
Zusammenfassung:
Nachdem in unserem Beispiel die beiden Rechtecke nicht ähnlich sind, können wir der Behauptung, dass Rechtecke immer ähnlich sind, widersprechen!
Die Ähnlichkeit beim Rechteck:
Rechtecke sind normalerweise nicht ähnlich zueinander.
Rechtecke sind normalerweise nicht ähnlich zueinander.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar