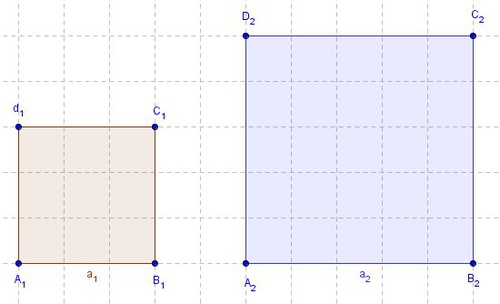
Ähnlichkeiten beim Quadrat

Quadrate sind immer ähnlich zueinander.

Ähnlichkeiten beim Quadrat

Beispiel

Wir wollen herausfinden, ob beliebige Quadrate immer ähnlich zueinander sind. Dazu konstruieren wir folgende Quadrate:

Quadrat 1: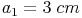 a_1 = 3\ cm

Quadrat 2: 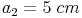a_2 = 5\ cm


Dazu vergleichen wir die Winkel und Seiten der beiden Quadrate miteinander.


Winkel:
Ähnlichkeit:

Entsprechende Winkel ähnlicher Figuren sind gleich groß.
(\alpha_1 = \alpha_2 , \beta_1 = \beta_2 , \gamma_1 = \gamma_2 , ...)

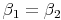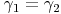Da in einem Quadrat jeder Winkel ein rechter Winkel ist (90°), stimmt diese Behauptung bei unseren beiden Quadraten!

\alpha_1 = \alpha_2, \beta_1 = \beta_2, \gamma_1 = \gamma_2 , \delta_1 = \delta_2


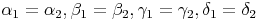
Seiten:
Ähnlichkeit:

Entsprechende Seiten ähnlicher Figuren sind proportional zueinander (haben das gleiche Verhältnis).
(a_1 : a_2 = 1 : 2 , b_1 : b_2 = 1 : 2 , c_1 : c_2 = 1 : 2 , ...)

\begin{align} & a_1 : a_2 = 5 : 7 \\ & b_1 : b_2 = 3 : 2 \end{align}

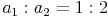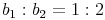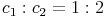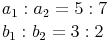
Die beiden Verhältnisse sind identisch, daher sind die beiden Quadrate auch ähnlich zueinander!


Zusammenfassung:

Die Winkeln aller Quadrate sind immer rechte Winkel (90°) und gleich groß. Da die Seiten in einem Quadrat immer gleich lang sind, die die Verhältnisse aller vier Seiten immer gleich.

Aus diesem Grund sind alle Quadrate ähnlich zueinander.

Die Ähnlichkeit beim Quadrat:

Quadrate sind immer ähnlich zueinander.

Kommentar verfassen