Ähnlichkeiten beim gleichseitigen Dreieck
Erfahren Sie mehr über das gleichseitige DreieckBeispiel:
Konstruieren Sie ein gleichseitiges Dreieck mit der Seitenlänge 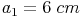 und anschließend ein zweites gleichseitiges Dreieck mit halber Seitenlänge! (
und anschließend ein zweites gleichseitiges Dreieck mit halber Seitenlänge! (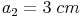 )
)
Da gleichseitige Dreiecke gleich große Winkel (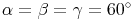 ) haben, haben alle gleichseitigen Dreiecke gleiche Gestalt, nur unterschiedliche Größe - sie sind also immer ähnlich!
) haben, haben alle gleichseitigen Dreiecke gleiche Gestalt, nur unterschiedliche Größe - sie sind also immer ähnlich!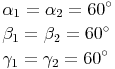
Da ein gleichseitige Dreieck drei gleich lange Seiten hat, werden alle Seiten mit a beschriftet!
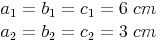
Verbindungsstrecken der Seitenmittelpunkte:
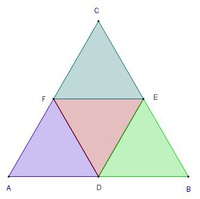
Halbiert man alle 3 Seiten und verbindet die dadurch entstandenen Punkte D, E und F miteinander, so ergeben sich 4 gleich große (kongruente) Dreiecke, die dem Ausgangsdreieck ähnlich sind.
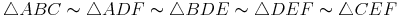
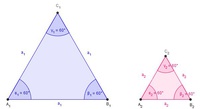
Gleichseitige Dreiecke haben drei gleich große Winkel (immer 60°). Daher sind sich alle gleichseitigen Dreiecke ähnlich!
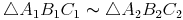
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Benji
Seht tolle Seite, hat mir sehr geholfen!