Ähnlichkeiten beim rechtwinkligen Dreieck
Beispiel:
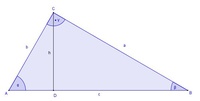
Konstruieren Sie ein rechtwinkeliges Dreieck mit der Hypotenuse 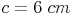 und dem Winkel
und dem Winkel 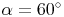 .
.
(Tipp: Da die Seite c die Hypotenuse unseres rechtwinkeligen Dreieckes ist, ist der gegenüberliegende Winkel Gamma ein rechter Winkel, also 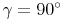 )
)
Zeichnen Sie nun auch die Höhe 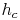 ein!
ein!
(Tipp: die Höhe steht normal auf die Seite und verläuft durch den gegenüberliegenden Eckpunkt)
Beweis 1:
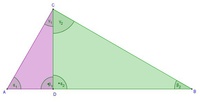
Die Höhe 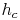 teilt das rechtwinkelige Dreieck in zwei kleinere Dreiecke.
teilt das rechtwinkelige Dreieck in zwei kleinere Dreiecke.
Beweisen Sie, dass diese beiden kleineren Dreiecke zueinander ähnlich sind!
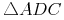 :
:
Aus der Angabe wissen wir: 
Da die Höhe normal auf die Seite steht, gilt: 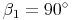
Die Winkelsumme im Dreieck beträgt 180°, daher gilt: 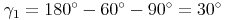
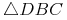 :
:
Da die Höhe normal auf die Seite steht, gilt: 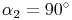
Im Eckpunkt C ist laut Angabe ein rechter Winkel, daher gilt: 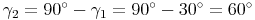
Die Winkelsumme im Dreieck beträgt 180°, daher gilt: 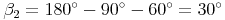
Vergleich 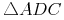 mit
mit 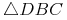 :
:
Wir versuchen nun gleich große Winkel zu finden:
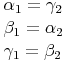
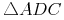 und
und 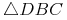 in allen 3 Winkeln übereinstimmen, sind sie zueinander ähnlich!
in allen 3 Winkeln übereinstimmen, sind sie zueinander ähnlich!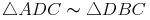
Beweis 2:
Die Höhe 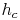 teilt das rechtwinkelige Dreieck in zwei kleinere Dreiecke.
teilt das rechtwinkelige Dreieck in zwei kleinere Dreiecke.
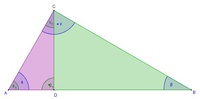
Beweisen Sie, dass das linke der beiden kleinen Dreiecke und das Ausgangsdreieck zueinander ähnlich sind!
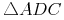 :
:
Aus der Angabe wissen wir: 
Da die Höhe normal auf die Seite steht, gilt: 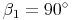
Die Winkelsumme im Dreieck beträgt 180°, daher gilt: 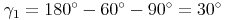
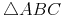 :
:
Aus der Angabe wissen wir: 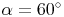
Am Beginn haben wir bereits herausgefunden, dass Gamma ein rechter Winkel ist, also: 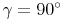
Die Winkelsumme im Dreieck beträgt 180°, daher gilt: 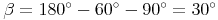
Vergleich 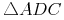 mit
mit 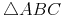 :
:
Wir versuchen nun gleich große Winkel zu finden:
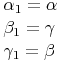
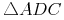 und
und 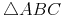 in allen 3 Winkeln übereinstimmen, sind sie zueinander ähnlich!
in allen 3 Winkeln übereinstimmen, sind sie zueinander ähnlich!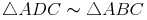
Beweis 3:
Die Höhe 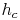 teilt das rechtwinkelige Dreieck in zwei kleinere Dreiecke.
teilt das rechtwinkelige Dreieck in zwei kleinere Dreiecke.
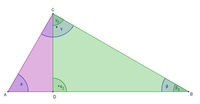
Beweisen Sie, dass das rechte der beiden kleinen Dreiecke und das Ausgangsdreieck zueinander ähnlich sind!
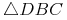 :
:
Da die Höhe normal auf die Seite steht, gilt: 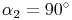
Im Eckpunkt C ist laut Angabe ein rechter Winkel, daher gilt: 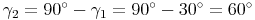
Die Winkelsumme im Dreieck beträgt 180°, daher gilt: 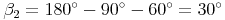
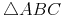 :
:
Aus der Angabe wissen wir: 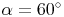
Am Beginn haben wir bereits herausgefunden, dass Gamma ein rechter Winkel ist, also: 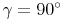
Die Winkelsumme im Dreieck beträgt 180°, daher gilt: 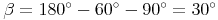
Vergleich 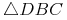 mit
mit 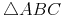 :
:
Wir versuchen nun gleich große Winkel zu finden:
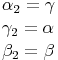
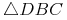 und
und 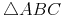 in allen 3 Winkeln übereinstimmen, sind sie zueinander ähnlich!
in allen 3 Winkeln übereinstimmen, sind sie zueinander ähnlich!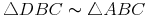
Unterteilt man das rechtwinklige Dreieck
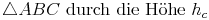 in zwei kleinere Dreiecke
in zwei kleinere Dreiecke 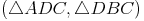 , so gilt:
, so gilt: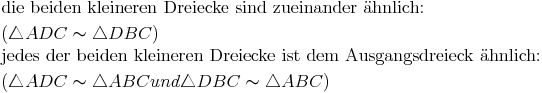
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar