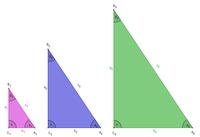
Flächeninhalte ähnlicher Figuren
Beispiel:
Konstruieren Sie ein rechtwinkeliges Dreieck, dessen Katheten 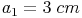 und
und 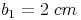 lang sein sollen.
lang sein sollen.
Als nächstes konstruieren Sie das gleiche Dreieck nochmals, allerdings mit doppelt so langen Kathetenlängen.
Schließlich konstruieren Sie das erste Dreieck nochmals, diesmal sollen die Katheten dreimal so lange sein.
Wir haben nun drei ähnliche Dreiecke, deren Flächeninhalte wir miteinander vergleichen wollen.
Der Flächeninhalt des rechtwinkeligen Dreiecks:
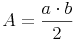
Flächeninhalt = (Kathete x Kathete) / 2
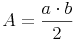
Flächeninhalt = (Kathete x Kathete) / 2
Mehr dazu: Flächeninhalt des rechtwinkeligen Dreiecks
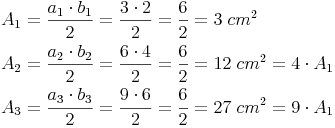
Verdoppelt man die Seitenlänge eines Dreieckes, so wird der Flächeninhalt vier Mal so groß.

Verdreifacht man die Seitenlänge eins Dreiecks, so wird der Flächeninhalt neun Mal so groß.

Flächeninhalte ähnlicher Figuren:
Die Flächeninhalte ähnlicher Figuren steigen wie die Quadrate entsprechender Seitenlängen an!
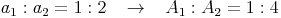
Die Flächeninhalte ähnlicher Figuren steigen wie die Quadrate entsprechender Seitenlängen an!
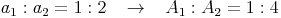
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar