Flächengleiche Rechtecke

Rechtecke, die trotz ihrer unterschiedlichen Seitenlängen denselben Flächeninhalt haben, müssen nicht auch zwingend umfanggleich sein.

Problemstellung:

Wir wollen herausfinden, ob Rechtecke mit gleichem Flächeninhalt auch den gleichen Umfang haben.

Beispiel:

Rechteck 1: l = 16 cm , b = 3 cm

Rechteck 2: l = 12 cm , b = 4 cm

Rechteck 3: l = 8 cm , b = 6 cm

Flächeninhalt des Rechtecks:

$A = l \cdot b$

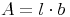
Flächenberechnungen: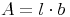

Rechteck 1: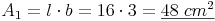
$A_1 = l \cdot b = 16 \cdot 3 = \underline{48\ cm^2}$

Rechteck 2: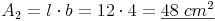
$A_2 = l \cdot b = 12 \cdot 4 = \underline{48\ cm^2}$

Rechteck 3: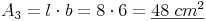
$A_3 = l \cdot b = 8 \cdot 6 = \underline{48\ cm^2}$

Zusammenfassung:
Alle 3 Rechtecke haben zwar unterschiedliche Seitenlängen, aber dieselben Flächeninhalte.

Umfang des Rechtecks:

u = l + b + l + b

$u = 2 \cdot l + 2 \cdot b$

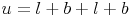
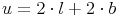
Umfangberechnungen: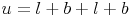

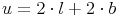
Rechteck 1: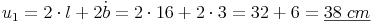
$u_1 = 2 \cdot l + 2 \dot b = 2 \cdot 16 + 2 \cdot 3 = 32 + 6 = \underline{38\ cm}$

Rechteck 2: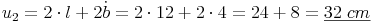
$u_2 = 2 \cdot l + 2 \dot b = 2 \cdot 12 + 2 \cdot 4 = 24 + 8 = \underline{32\ cm}$

Rechteck 3: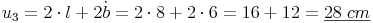
$u_3 = 2 \cdot l + 2 \dot b = 2 \cdot 8 + 2 \cdot 6 = 16 + 12 = \underline{28\ cm}$

Zusammenfassung:
Alle 3 Rechtecke haben den nicht den gleichen Umfang.

Fazit:

Rechtecke, die trotz ihrer unterschiedlichen Seitenlängen denselben Flächeninhalt haben, müssen nicht zwingend auch umfanggleich sein.

Rechtecke mit gleichem Flächeninhalt müssen nicht denselben Umfang haben.