Rechteck: Umfanggleiche Rechtecke

Rechtecke, die trotz ihrer unterschiedlichen Seitenlängen denselben Umfang haben, müssen nicht auch zwingend flächengleich sein.

Umfanggleiche Rechtecke

Problemstellung:

Wir wollen herausfinden, ob Rechtecke mit gleichem Umfang auch den gleichen Flächeninhalt haben.

Beispiel:

Rechteck 1: l = 10 cm , b = 8 cm

Rechteck 2: l = 12 cm , b = 6 cm

Rechteck 3: l = 15 cm , b = 3 cm

Umfang des Rechtecks:

u = l + b + l + b

$u = 2 \cdot l + 2 \cdot b$

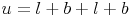
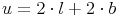
Umfangberechnungen: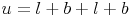

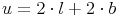
Rechteck 1:
$u_1 = 2 \cdot l + 2 \cdot b = 2 \cdot 10 + 2 \cdot 8 = 20 + 16 = \underline{36\ cm}$

Rechteck 2:
$u_2 = 2 \cdot l + 2 \cdot b = 2 \cdot 12 + 2 \cdot 6 = 24 + 12 = \underline{36\ cm}$

Rechteck 3: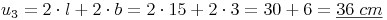
$u_3 = 2 \cdot l + 2 \cdot b = 2 \cdot 15 + 2 \cdot 3 = 30 + 6 = \underline{36\ cm}$

Zusammenfassung:
Alle 3 Rechtecke haben zwar unterschiedliche Seitenlängen, aber den gleichen Umfang.

Flächeninhalt des Rechtecks:

$A = l \cdot b$

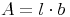
Flächenberechnungen:

Rechteck 1: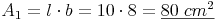
$A_1 = l \cdot b = 10 \cdot 8 = \underline{80\ cm^2}$

Rechteck 2: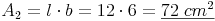
$A_2 = l \cdot b = 12 \cdot 6 = \underline{72\ cm^2}$

Rechteck 3: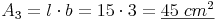
$A_3 = l \cdot b = 15 \cdot 3 = \underline{45\ cm^2}$

Zusammenfassung:
Alle 3 Rechtecke haben unterschiedliche Flächeninhalte.

Fazit:

Rechtecke, die trotz ihrer unterschiedlichen Seitenlängen denselben Umfang haben, müssen nicht zwingend auch flächengleich sein.

Rechtecke mit gleichem Umfang müssen nicht denselben Flächeninhalt haben.

Kommentar #42490 von Lisa 03.04.19 17:12 Lisa: Kann mir jemand den Grund dafür nennen? Warum ist der Umfang immer derselbe,trotz unterschiedlicher Fläche?