Der Inkreis des Tangentenvierecks
Man kann jedem Tangentenviereck einen Kreis einschreiben, der alle 4 Seitenflächen berührt (= Inkreis)
Um herauszufinden, ob es sich bei einem allgemeinen Viereck um ein Tangentenviereck handelt, wendet man am besten die Seitenformel (a + c = b + d) an. Wenn diese gilt, so handelt es sich um ein Tangentenviereck.
Um den Inkreis zu erhalten, müssen die Winkelsymmetralen des Tangentenvierecks konstruiert werden. Diese werden mit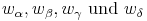 
bezeichnet.
Die Winkelsymmetrale halbiert einen Winkel.
Der Schnittpunkt der Winkelsymmetralen ist der Mittelpunkt (M) des Inkreises. Er ist also von allen 4 Seiten gleich weit entfernt.
Der Inkreisradius ist der kürzeste Abstand (Normalabstand) einer beliebigen Seite des Tangentenvierecks zum Mittelpunkt M. Um diesen zu erhalten, zeichnen Sie eine Normale auf eine Seite durch den Mittelpunkt.
Der Inkreis eines Tangentenvierecks
Jedes Tangentenviereck besitzt einen Inkreis.
Der Inkreismittelpunkt ist der Schnittpunkt der Winkelsymmetralen des Tangentenvierecks.
Der Inkreisradius r ist der Normalabstand des Inkreismittelpunktes M zu einer beliebigen Seite.
Jedes Tangentenviereck besitzt einen Inkreis.
Der Inkreismittelpunkt ist der Schnittpunkt der Winkelsymmetralen des Tangentenvierecks.
Der Inkreisradius r ist der Normalabstand des Inkreismittelpunktes M zu einer beliebigen Seite.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Grabenberger Lara
Es hat mir kein bischen geholfen