Die Seiten des Tangentenvierecks
Ein Tangentenviereck hat normalerweise vier unterschiedlich lange Seiten, die normalerweise auch weder parallel verlaufen noch normal aufeinander stehen.
Dennoch weist ein Tangentenviereck die Besonderheit auf, dass die Summe der Längen der gegenüberliegenden Seiten gleich ist, also: a + c = b + d
Beweis:
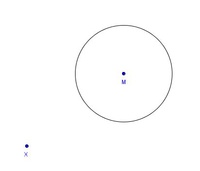
Schritt 1:Wir konstruieren einen Teil eines Tangentenviereckes, nämlich den Inkreis und einen beliebigen Eckpunkt, den wir mit X bezeichnen.
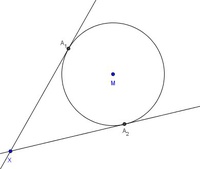
Schritt 2:
Wir konstruieren vom Punkt X aus die beiden Tangenten an den Inkreis.
Die beiden Berührungspunkte bezeichnen wir als 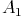 und
und 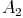
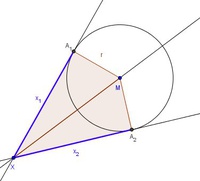
Schritt 3:
Verbindet man den Punkt X mit dem Punkt M des Inkreises, so kann man erkennen, dass eine Symmetrieachse entstanden ist.
Zur besseren Veranschaulichung malen wir die entstandenen Dreiecke 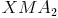 und
und 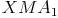 färbig an.
färbig an.
Beide Dreiecke sind gleich groß, deshalb sind auch die beiden Strecken von X bis zu den Berührungspunkten 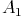 und
und 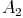 gleich lang. Wir benennen sie mit
gleich lang. Wir benennen sie mit 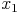 und [[FORMEL]].
und [[FORMEL]].
Es gilt also: 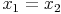
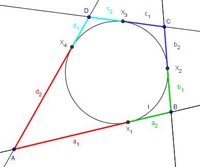
Schritt 4:
Die soeben erarbeitete Erkenntnis gilt natürlich für alle 4 Eckpunkte des Tangentenvierecks. Zwecks besserer Übersicht haben wir Ihnen die jeweils gleich langen Streckenabschnitte gleich färbig gemacht.
Da es von jeder Farbe 2 Strecken gibt, teilen wir mal durch 2:
Wir addieren eine rote, eine grüne (beide zusammen entsprechen der Seite a), eine hellblaue und eine dunkelblaue Strecke (beide zusammen entsprechen der Seite a): 
Wir addieren außerdem eine grüne, eine dunkelblaue (beide zusammen entsprechen der Seite b), eine hellblaue und eine rote Strecke (beide zusammen entsprechen der Seite d): 
Beide Additionen sind gleich, also kann man sie mit einem =Zeichen anschreiben: 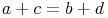
In einem Tangentenviereck ist die Summe der Längen der gegenüberliegenden Seiten gleich.
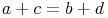
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar