Das Assoziativgesetz beim Multiplizieren mit natürlichen Zahlen
Beim Malrechnen dürfen wir die einzelnen Faktoren beliebig zu Teilprodukten verbinden. Das besagt das Assoziativgesetz (= Verbindungsgesetz).
Beispiel:
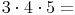
Rechengang 1: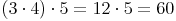
Rechengang 2: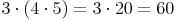
Bei beiden Rechenvarianten kommen wir zum selben Ergebnis!
Assoziativgesetz (Verbindungsgesetz) bei der Multiplikation:
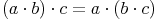
Die Faktoren können beliebig zu Teilprodukten verbunden werden
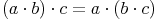
Die Faktoren können beliebig zu Teilprodukten verbunden werden
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar