Kubikwurzeln von Quotienten

Dividiert man die Kubikwurzeln zweier Zahlen, so erhält man dasselbe Ergebnis wie beim Kubikwurzelziehen des Quotienten der beiden Zahlen.

Kubikwurzelziehen von Quotienten

Hier wollen wir folgende Gesetzmäßigkeit überprüfen:

\sqrt[3]{a : b}\quad \overset{?}{=}\quad \sqrt[3]{a} : \sqrt[3]{b}

Es gilt: a, b \in \mathbb R \quad , \quad b \not= 0

Beispiel:

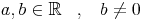
Prüfen Sie, ob das =Zeichen korrekt gesetzt wurde oder nicht!

\sqrt[3]{1\ 000 : 125} \overset{?}{=} \sqrt[3]{1\ 000} : \sqrt[3]{125}

Nun berechnen wir gleichzeitig sowohl die linke als auch die rechte Seite des =Zeichens:

\begin{align} & \sqrt[3]{8} \overset{?}{=} \sqrt[3]{1\ 000} \cdot \sqrt[3]{125} \\ & 2 \overset{?}{=} 10 : 5 \\ \end{align}

Die beiden Ergebnisse stimmen überein, daher können wir nun das ? über dem =Zeichen weglassen:

2 = 2

Kubikwurzelziehen von Quotienten:

Dividiert man die Kubikwurzeln zweier Zahlen, so erhält man dasselbe Ergebnis wie beim Kubikwurzelziehen des Quotienten der beiden Zahlen:

\sqrt[3]{a : b}\quad = \quad \sqrt[3]{a} : \sqrt[3]{b}

Kommentar verfassen