Teilweises Kubikwurzelziehen (Partielles Kubikwurzelziehen)
Beispiel:
![\sqrt[3]{128} = \sqrt[3]{128} =](/media/formulas/79dc8a74da3487a121b59748fb31a3a5.png)
Wir zerlegen die Zahl 128 in ein Produkt, wobei ein man von einem Faktor davon die Kubikwurzel ziehen können soll.
64 ist eine mögliche Zahl, da 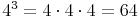
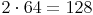
Daher gilt:
![\sqrt[3]{128} = \sqrt[3]{2 \cdot 64} \sqrt[3]{128} = \sqrt[3]{2 \cdot 64}](/media/formulas/4c39373388dfcd5e6dabc93211c203a9.png)
Wir wenden nun folgende Gesetzmäßigkeit an:
Kubikwurzelziehen von Produkten:
![\sqrt[3]{a \cdot b}\quad = \quad \sqrt[3]{a} \cdot \sqrt[3]{b} \sqrt[3]{a \cdot b}\quad = \quad \sqrt[3]{a} \cdot \sqrt[3]{b}](/media/formulas/be54af8b00f6a7f457b7b3c14e337936.png)
![\sqrt[3]{a \cdot b}\quad = \quad \sqrt[3]{a} \cdot \sqrt[3]{b} \sqrt[3]{a \cdot b}\quad = \quad \sqrt[3]{a} \cdot \sqrt[3]{b}](/media/formulas/be54af8b00f6a7f457b7b3c14e337936.png)
Weitere Infos: Kubikwurzelziehen von Produkten
Diese Regel übertragen wir nun auf unser Beispiel:
![\sqrt[3]{128} = \sqrt[3]{2 \cdot 64} = \sqrt[3]{2} \cdot \sqrt[3]{64} = \sqrt[3]{128} = \sqrt[3]{2 \cdot 64} = \sqrt[3]{2} \cdot \sqrt[3]{64} =](/media/formulas/13e5b7f31fa8e85e48df6263dec89c51.png)
Nun können wir partiell (teilweise) Wurzelziehen:
![\sqrt[3]{128} = \sqrt[3]{2 \cdot 64} = \sqrt[3]{2} \cdot \sqrt[3]{64} = \underline{4 \cdot \sqrt[3]{2}} \sqrt[3]{128} = \sqrt[3]{2 \cdot 64} = \sqrt[3]{2} \cdot \sqrt[3]{64} = \underline{4 \cdot \sqrt[3]{2}}](/media/formulas/2389ad57716c2a0919e1332b9706c256.png)
Teilweises Kubikwurzelziehen (Partielles Kubikwurzelziehen:
Wenn unter dem Wurzelzeichen Faktoren stehen, die Kubikzahlen sind, so kann man die Kubikwurzel ziehen.
Wenn unter dem Wurzelzeichen Faktoren stehen, die keine Kubikzahlen sind, so bleiben sie unter dem Wurzelzeichen stehen.
z.B.:![\sqrt[3]{125 \cdot 3} = \sqrt[3]{125} \cdot \sqrt[3]{3} = 5 \cdot \sqrt[3]{3} \sqrt[3]{125 \cdot 3} = \sqrt[3]{125} \cdot \sqrt[3]{3} = 5 \cdot \sqrt[3]{3}](/media/formulas/25680e62793685dbddb5cd068b9b1ca7.png)
Weitere Beispiele:Wenn unter dem Wurzelzeichen Faktoren stehen, die Kubikzahlen sind, so kann man die Kubikwurzel ziehen.
Wenn unter dem Wurzelzeichen Faktoren stehen, die keine Kubikzahlen sind, so bleiben sie unter dem Wurzelzeichen stehen.
z.B.:
![\sqrt[3]{125 \cdot 3} = \sqrt[3]{125} \cdot \sqrt[3]{3} = 5 \cdot \sqrt[3]{3} \sqrt[3]{125 \cdot 3} = \sqrt[3]{125} \cdot \sqrt[3]{3} = 5 \cdot \sqrt[3]{3}](/media/formulas/25680e62793685dbddb5cd068b9b1ca7.png)
![\begin{align} & \sqrt[3]{343 \cdot 8 \cdot 5} = \sqrt[3]{343} \cdot \sqrt[3]{8} \cdot \sqrt[3]{5} = 7 \cdot 2 \cdot \sqrt[3]{5} = \underline{14 \cdot \sqrt[3]{5}} \\ & \sqrt[3]{27 \cdot x^3 \cdot y} = \sqrt[3]{27} \cdot \sqrt[3]{x^3} \cdot \sqrt[3]{y} = 3 \cdot x \cdot \sqrt[3]{y} = \underline{3x \cdot \sqrt[3]{y}} \\ \end{align} \begin{align} & \sqrt[3]{343 \cdot 8 \cdot 5} = \sqrt[3]{343} \cdot \sqrt[3]{8} \cdot \sqrt[3]{5} = 7 \cdot 2 \cdot \sqrt[3]{5} = \underline{14 \cdot \sqrt[3]{5}} \\ & \sqrt[3]{27 \cdot x^3 \cdot y} = \sqrt[3]{27} \cdot \sqrt[3]{x^3} \cdot \sqrt[3]{y} = 3 \cdot x \cdot \sqrt[3]{y} = \underline{3x \cdot \sqrt[3]{y}} \\ \end{align}](/media/formulas/10545345cb1ccdcd4c29c83f9549a95c.png)
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar