Kubikwurzelziehen von Summen
Hier wollen wir folgende Gesetzmäßigkeit überprüfen:
![\sqrt[3]{a + b}\quad \overset{?}{=}\quad \sqrt[3]{a} + \sqrt[3]{b}](/media/formulas/9aa28d47217da1075e8a5569e9818c06.png "\sqrt[3]{a + b}\quad \overset{?}{=}\quad \sqrt[3]{a} + \sqrt[3]{b}")
Es gilt: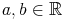 
Prüfen Sie, ob das =Zeichen korrekt gesetzt wurde oder nicht!
![\sqrt[3]{27 + 64} \overset{?}{=} \sqrt[3]{27} + \sqrt[3]{64}](/media/formulas/49c3c4f1e0fde29185a070b3e824413e.png "\sqrt[3]{27 + 64} \overset{?}{=} \sqrt[3]{27} + \sqrt[3]{64}")
Nun berechnen wir gleichzeitig sowohl die linke als auch die rechte Seite des =Zeichens:
![\begin{align} & \sqrt[3]{91} \overset{?}{=} \sqrt[3]{27} + \sqrt[3]{64} \\ & 4,5 \overset{?}{=} 3 + 4 \\ \end{align}](/media/formulas/0e72ae6bfb0735defa8a42c0f1c85059.png "\begin{align} & \sqrt[3]{91} \overset{?}{=} \sqrt[3]{27} + \sqrt[3]{64} \\ & 4,5 \overset{?}{=} 3 + 4 \\ \end{align}")
Die beiden Ergebnisse stimmen nicht überein, daher setzen wir nun auch kein =Zeichen mehr:
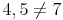
Kubikwurzelziehen von Summen:
Addiert man die Kubikwurzeln zweier Zahlen, so erhält man ein anderes Ergebnis als beim Kubikwurzelziehen der Summe der beiden Zahlen:
![\sqrt[3]{a + b}\quad \not= \quad \sqrt[3]{a} + \sqrt[3]{b}](/media/formulas/2c6192db6cad262692ef462e05f56d12.png "\sqrt[3]{a + b}\quad \not= \quad \sqrt[3]{a} + \sqrt[3]{b}")
Addiert man die Kubikwurzeln zweier Zahlen, so erhält man ein anderes Ergebnis als beim Kubikwurzelziehen der Summe der beiden Zahlen:
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar