Berechnung des Flächeninhaltes eines Kreisrings
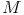 .......... Mittelpunkt beider Kreise
.......... Mittelpunkt beider Kreise
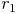 ........... Radius des größeren Kreises
........... Radius des größeren Kreises
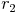 .......... Radius des kleineren Kreises
.......... Radius des kleineren Kreises
Herleitung der Formel
Aus dem vorherigen Kapitel kennen wir bereits die Formel zur Berechnung des Flächeninhalts eines Kreises:
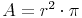
Der Flächeninhalt des Kreisringes ergibt sich eigentlich daraus, dass aus der Fläche des größeren Kreises ein Loch (Fläche des kleineren Kreises) herausgestanzt wird.
Rechnerisch bedeutet dies, dass man von der Kreisfläche des größeren Kreises die Kreisfläche des kleineren Kreises abzieht - dann bleibt nur die Fläche des Kreisrings übrig:
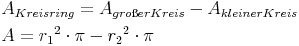
In jeder der beiden Flächenformeln kommt 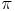 vor, deshalb bietet es sich an,
vor, deshalb bietet es sich an, 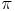 herauszuheben, um die Formel eleganter und kürzer zu gestalten:
herauszuheben, um die Formel eleganter und kürzer zu gestalten:
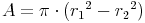
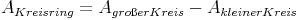
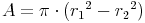
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
