Formelsammlung Kreisring
Ein Kreisring ist von zwei konzentrischen Kreisen begrenzt. Konzentrische Kreise haben denselben Mittelpunkt, aber verschiedene Radien.
Hier finden Sie eine Zusammenfassung aller wichtigen Formeln für Berechnungen zum Thema "Kreisring". Genauere Erklärungen zu den einzelnen Formeln finden Sie in den entsprechenden Kapiteln.
Umfang:
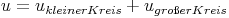
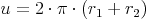
Umfang - Umkehraufgaben:
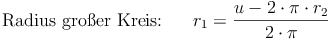
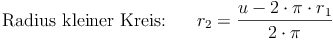
Flächeninhalt:
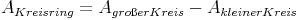
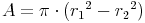
Flächeninhalt - Umkehraufgaben:
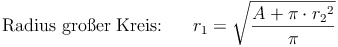
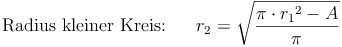
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar