Berechnung des Umfangs eines Kreisrings
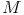 .......... Mittelpunkt beider Kreise
.......... Mittelpunkt beider Kreise
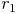 ........... Radius des größeren Kreises
........... Radius des größeren Kreises
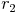 .......... Radius des kleineren Kreises
.......... Radius des kleineren Kreises
Herleitung der Formel
Aus dem vorherigen Kapitel kennen wir bereits die Formel zur Berechnung des Kreisumfangs:
Kreisumfang: 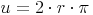
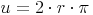
Ein Kreisring ist von 2 unterschiedlich großen Kreisen umgeben. Daher setzt sich der Umfang des Kreisrings aus der Summe der beiden Umfänge der Kreise zusammen:
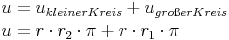
In jedem der beiden Summanden kommt 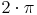 vor, deshalb bietet es sich an,
vor, deshalb bietet es sich an, 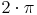 herauszuheben, um die Formel eleganter und kürzer zu gestalten:
herauszuheben, um die Formel eleganter und kürzer zu gestalten:
Dreht man die beiden Summanden in der Klammer um, so erhält man:
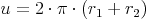
Umfang des Kreisrings:
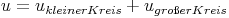
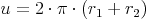
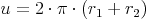
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
