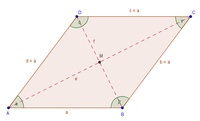
Die Raute (der Rhombus)
Eine Raute (ein Rhombus) ist ein Parallelogramm mit 4 gleich langen Seiten.
Die Beschriftung der Eckpunkte erfolgt mit Großbuchstaben und gegen den Uhrzeigersinn: A, B, C, D
Die Beschriftung der Seiten erfolgt mit Kleinbuchstaben und gegen den Uhrzeigersinn: a, b, c, d
Die Beschriftung der Winkel erfolgt mit griechischen Kleinbuchstaben, passend zum Eckpunkt:
Winkel 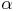 [sprich: Alpha] beim Eckpunkt A
[sprich: Alpha] beim Eckpunkt A
Winkel 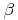 [sprich: Beta] beim Eckpunkt B
[sprich: Beta] beim Eckpunkt B
Winkel 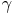 [sprich: Gamma] beim Eckpunkt C
[sprich: Gamma] beim Eckpunkt C
Winkel 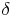 [sprich: Delta] beim Eckpunkt D
[sprich: Delta] beim Eckpunkt D
Die Beschriftung der Diagonalen erfolgt mit Kleinbuchstaben: e, f
Die Diagonale e verbindet die Eckpunkte A und C
Die Diagonale f verbindet die Eckpunkte B und D
Die Diagonalen schneiden einander im Mittelpunkt M
In einer Raute (Rhombus) sind:
- die gegenüberliegenden Winkel gleich groß: ,
, 
- die benachbarten Winkel supplementär (=ergänzen einander auf 180°):
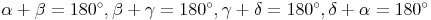
Die Diagonalen halbieren einander und stehen aufeinander normal.
- die gegenüberliegenden Winkel gleich groß:
 ,
, 
- die benachbarten Winkel supplementär (=ergänzen einander auf 180°):
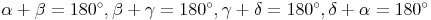
Die Diagonalen halbieren einander und stehen aufeinander normal.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
aRii..
Gut. :D Denn ich habe morgen Mathe-Schularbeit. und hab mich da überhaupt nicht ausgekannt!!
aNiii
e=8cm
f=5cm
a=?
Wie geht das o.o
nini
wäre nett wenn dabei stehn würde wie man es konstruiert
Chiara
aNiii
Du musst e und f halbieren, und dann sind sie die zwei Katheten und a ist dann die Hypothenuse eines Dreiecks. Dann musst du nur mehr den Satz des Pythagoras anwenden. Das heißt: a²=(e/2)²+(f/2)²
Günther
ICH MUSSTE EIN PORTFOLIO FÜR MATHEMACHEN ::: HATTE ES NÄMLICH VEGESSEN ::: WUSSTE DANN NICHT WIE MAN EIEN RAUTE KONSTRUIERT ::: HAT SEH GEHOLFEN
Baran Kutlu
Was ist die formel von e' und f'?