Winkel

In einer Raute (einem Rhombus) beträgt die Winkelsumme so wie in jedem anderen Viereck 360°. Gegenüberliegende Winkel sind gleich groß.

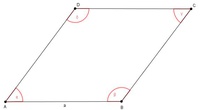
Die Winkel der Raute (des Rhombus)

In einer Raute (einem Rhombus) beträgt die Winkelsumme so wie in jedem anderen Viereck 360°.

Da gegenüberliegende Seiten einer Raute sowohl gleich lang sind als auch parallel zueinander verlaufen, sind auch gegenüberliegende Winkel gleich groß:
\alpha = \gamma (Alpha = Gamma)
\beta = \delta (Beta = Delta)

Winkelberechnung in einer Raute (einem Rhombus)

Beispiel:

geg.: Raute: 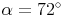\alpha = 72^\circ

Berechnen Sie die Größen der drei anderen Winkel!

\alpha + \beta + \gamma + \delta = 360^\circ

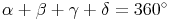
Da die gegenüberliegenden Winkel 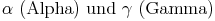\alpha \text{ (Alpha) und } \gamma \text{ (Gamma) } gleich groß sind und auch die gegenüberliegenden Winkel 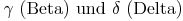\gamma \text{ (Beta) und } \delta \text{ (Delta) } gleich groß sind, können wir die obige Formel umformen:

\begin{align} & \alpha + \beta + \alpha+ \beta= 360^\circ \\ & 2 \cdot \alpha + 2 \cdot \beta = 360^\circ \end{align}

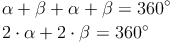
Wir setzen die Angabe in unsere Formel ein und formen um:

\begin{align} & 2 \cdot 72^\circ + 2 \cdot \beta = 360^\circ \\ & 144^\circ + 2 \cdot \beta = 360^\circ \qquad / - 144^\circ \\ & 2 \cdot \beta = 360^\circ - 144^\circ \\ & 2 \cdot \beta = 216^\circ \qquad / : 2 \\ & \beta = 216^\circ : 2 \\ & \beta = 108^\circ \\ \end{align}

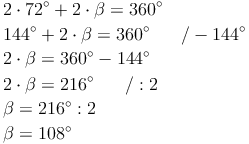
Da Gamma genauso groß ist wie Alpha, gilt: 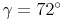\gamma = 72^\circ

Da Delta genauso groß ist wie Beta, gilt: 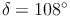\delta = 108^\circ

Probe: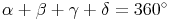

\alpha + \beta + \gamma + \delta = 360^\circ
72^\circ + 108^\circ + 72^\circ + 108^\circ = 360^\circ
360^\circ = 360^\circ

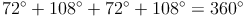
wahre Aussage!

Die Winkel in einer Raute (einem Rhombus):

In einer Raute beträgt die Winkelsumme so wie in jedem anderen Viereck 360°.

Gegenüberliegende Winkel sind gleich groß:
\alpha = \gamma (Alpha = Gamma)
\beta = \delta (Beta = Delta).

Kommentar verfassen