Formelsammlung Raute

Hier finden Sie eine Zusammenfassung aller wichtigen Formeln für Berechnungen in der Raute (im Rhombus).

Formeln für Berechnungen in der Raute

Hier finden Sie eine Zusammenfassung aller wichtigen Formeln für Berechnungen in der Raute (dem Rhombus). Die Seitenlängen wurden dazu immer mit a bezeichnet.

Winkel:

$\begin{align} \alpha + \beta = 180^\circ \\ \beta + \gamma = 180^\circ \\ \gamma + \delta = 180^\circ \\ \delta + \alpha = 180^\circ \\ \alpha + \beta + \gamma + \delta = 360^\circ\end{align}$

Umfang:

$u = 4 \cdot a$

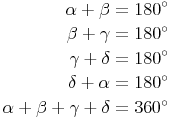
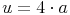
Umfang - Umkehraufgaben:

$a = \frac{u}{4}$

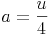
Flächeninhalt:

$A = a \cdot h$

$A= \frac{e \cdot f}{2}$

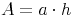
Flächeninhalt - Umkehraufgaben:

$a = \frac{A}{h}$
$h = \frac{A}{a}$

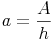
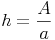
Seitenlänge bzw. Diagonalen:

$a = \sqrt{\left ( \frac{e}{2}\right )^2 + \left ( \frac{f}{2}\right )^2}$

$e = 2 \cdot \sqrt{a^2 - \left ( \frac{f}{2}\right )^2}$

$f = 2 \cdot \sqrt{a^2 - \left ( \frac{e}{2}\right )^2}$

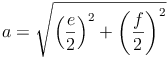
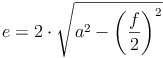
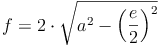
Dieser Artikel hat mir geholfen. das half mir
... leider nicht ... leider nicht
Kommentar Kommentar
2,8
567 Bewertungen

Kommentar #14604 von Alwin Brucie 30.04.16 15:17 Alwin Brucie: Ich muss folgentes rechnen:
A=789a
d=525
und das die seite a=?.