Berechnung der Seitenlänge der Raute, wenn der Umfang bekannt ist
Von einer Umkehraufgabe sprechen wir, wenn der Umfang der Raute bereits gegeben ist, aber die Seitenlänge unbekannt.
Man muss nun die Umfangsformel so umformen, dass man sich die unbekannte Seite berechnen kann.
Beispiel:
Von einer Raute kennt man den Umfang u = 44 cm. Berechnen Sie die Länge der Seite a!
Herleitung der Formel:
Aus
dem vorherigen Kapitel wissen wir bereits, dass der Umfang einer Raute die Summe der vier Seiten ist. Da in einer Raute alle vier Seiten gleich lang sind,
gilt:
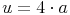
Nachdem wir den Umfang der Raute kennen, die Seite a allerdings nicht, formen wir unsere Formel so um, bis die Seite a allein auf einer Seite steht: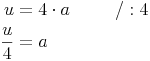
Beispiel (Forts.):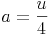
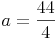
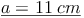
Probe: Wir setzen das Ergebnis in die Umfangsformel ein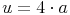
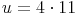
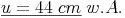
Antwort:
Die Seite a der Raute ist 11 cm lang.
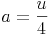
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Kira
Ich hab nicht das gefunden was ich suche, gibt es hier auch Angaben ,wie man a berechnet nur mit dem Flächeninhalt?