Der Umkreis eines geleichschenkligen Trapezes
Im Gegensatz zum allgemeinen Trapez, bei dem kein Umkreis existiert, kann man beim gleichschenkligen Trapez sehr wohl einen Umkreis konstruieren.
Der Umkreis berührt alle 4 Eckpunkte A, B, C und D, sein Mittelpunkt ergibt sich aus dem Schnittpunkt der 4 Seitensymmetralen, wobei die Seitensymmetralen der beiden Parallelseiten a und c identisch sind.
Im Folgenden geben wir Ihnen eine Anleitung zur Kontruktion des Umkreises eines gleichschenkligen Trapezes - Schritt für Schritt.
Schritt 1:
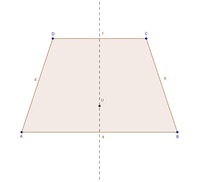
Wir konstruieren die Seitensymmetrale der Seite a.
Dazu halbieren wir die Seite a und zeichnen eine Normale auf diese.
Da es sich um ein gleichschenkliges Trapez handelt, ist die Seitensymmetrale der Seite a identisch mit jender ihrer Parallelseite c.
Schritt 2:
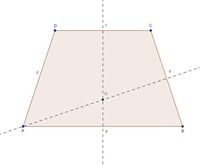
Nun wird die Seitensymmetrale der Seite b konstruiert.
Sie trifft sich mit jener der Seite a in einem Punkt, dem Umkreismittelpunkt. Der Genauigkeit und Vollständigkeit halber konstruieren wir allerdings noch die Seitensymmetralen der restlichen Seiten.
Schritt 3:
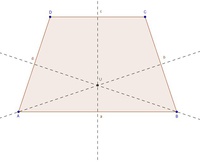
Die Streckensymmetrale der Seite c ist ja bereits konstruiert worden, da sie identisch mit jener der Seite a ist.
Also wird zuletzt noch die Seitensymmetrale der Seite d konstruiert.
Schritt 4:
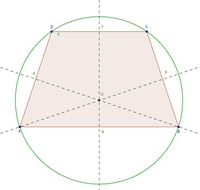
Die 4 Seitensymmetralen schneiden sich in einem Punkt, dem Umkreismittelpunkt.
Stechen Sie hier nun mit dem Zirkel ein, spannen Sie ihn bis zu einem der 4 Eckpunkte und zeichnen Sie den Umkreis.
Nur beim gleichschenkligen (nicht beim allgemeinen) Trapez existiert ein Umkreis. Den Umkreismittelpunkt erhaltet man durch die Konstruktion der Seitensymmetralen.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Anon
Danke, nützlich und Hilfreich!
- Ein Lehrer