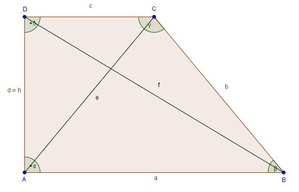
Das rechtwinklige Trapez
Rechtwinkliges Trapez:
Ein rechtwinkliges Trapez ist ein besonderes Trapez, bei dem einer der beiden Schenkel normal auf die beiden Parallelseiten steht. Dieser Schenkel bildet zugleich die Höhe.
d = h
Ein rechtwinkliges Trapez ist ein besonderes Trapez, bei dem einer der beiden Schenkel normal auf die beiden Parallelseiten steht. Dieser Schenkel bildet zugleich die Höhe.
d = h
Die Beschriftung der Eckpunkte erfolgt mit Großbuchstaben und gegen den Uhrzeigersinn: A, B, C, D
Die Beschriftung der Seiten erfolgt mit Kleinbuchstaben und gegen den Uhrzeigersinn: a, b, c, d (wobei d der Höhe h entspricht, also: d = h)
Die Winkel 
und 
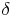in einem rechtwinkligen Trapez sind rechte Winkel (haben also jeweils 90°).
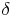und in einem rechtwinkligen Trapez sind rechte Winkel (haben also jeweils 90°).
Die Beschriftung der Diagonalen erfolgt mit Kleinbuchstaben: e, f
Die Diagonale e verbindet die Eckpunkte A und C
Die Diagonale f verbindet die Eckpunkte B und D
Die Diagonalen schneiden einander im Mittelpunkt M
Die Beschriftung der Winkel erfolgt mit griechischen Kleinbuchstaben, passend zum Eckpunkt: ![\begin{align}
& \text{ Winkel } {\alpha} \text{ [sprich: Alpha] beim Eckpunkt A} \\
& \text{ Winkel } {\beta} \text{ [sprich: Beta] beim Eckpunkt B} \\
& \text{ Winkel } {\gamma} \text{ [sprich: Gamma] beim Eckpunkt C} \\
& \text{ Winkel } {\delta} \text{ [sprich: Delta] beim Eckpunkt D }
\end{align}](/media/formulas/cdec052239b6f71301ffec145571b9b3.png "\begin{align}
& \text{ Winkel } {\alpha} \text{ [sprich: Alpha] beim Eckpunkt A} \\
& \text{ Winkel } {\beta} \text{ [sprich: Beta] beim Eckpunkt B} \\
& \text{ Winkel } {\gamma} \text{ [sprich: Gamma] beim Eckpunkt C} \\
& \text{ Winkel } {\delta} \text{ [sprich: Delta] beim Eckpunkt D }
\end{align}")
Die Winkel und 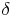sind rechte Winkel.
In einem rechtwinkligen Trapez:
- werden die parallelen Seiten (a und c) als Parallelseiten bezeichnet.
- werden die beiden nicht parallelen Seiten (b und d) als Schenkel bezeichnet, wobei d der Höhe h entspricht: d = h
- sind die beiden Diagonalen e und f unterschiedlich lang.
- sind die beiden am Schenkel d anliegenden Winkel rechte Winkel:
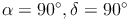
- werden die parallelen Seiten (a und c) als Parallelseiten bezeichnet.
- werden die beiden nicht parallelen Seiten (b und d) als Schenkel bezeichnet, wobei d der Höhe h entspricht: d = h
- sind die beiden Diagonalen e und f unterschiedlich lang.
- sind die beiden am Schenkel d anliegenden Winkel rechte Winkel:
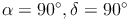
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar