Der Flächeninhalt des rechtwinkligen Trapezes
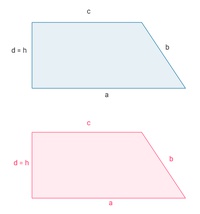
Herleitung der Flächeninhaltsformel:1) Wir konstruieren zwei beliebige gleich große rechtwinklige Trapeze.
2) Nun werden die Seitenlängen beschriftet, wobei die Seite d der Höhe h entspricht.
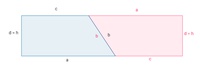
3) Das 1. Trapez bleibt liegen, das 2. Trapez wird so"umgelegt", dass die beiden Schenkel b übereinander liegen.
4) Ein Rechteck ist entstanden, dessen Fläche noch immer so groß ist wie jene der beiden ursprünglichen Trapeze zusammen.
5) Berechnung der Fläche des Rechtecks:
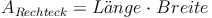
Die Länge des Rechtecks entspricht der Summe der Seiten a und c, die Breite entspricht der Seite d bzw. der Höhe h:
Länge: 
Breite: 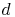 oder
oder 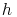
Setzt man dies in die Flächeninhaltsformel des Rechtecks ein, so ergibt sich:
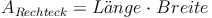
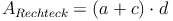 oder
oder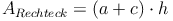
Die Fläche von einem der beiden Trapeze ist halb so groß wie jene des Rechtecks:
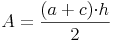 oder
oder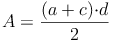
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Timo
Sehr gut liebe euch!