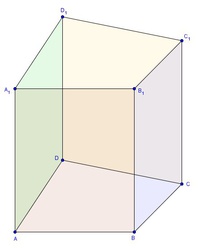
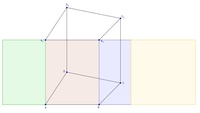
Die Oberfläche des vierseitigen Prismas
Ein vierseitiges Prisma besteht aus der Grundfläche und der kongruenten Deckfläche sowie 4 unterschiedlichen Seitenflächen, die zusammen den Mantel bilden.
Die Oberfläche setzt sich nun aus diesen 6 Flächen zusammen. Die Grund- und Deckfläche sind kongruent, daher fassen wir sie als Grundfläche zusammen. Die 4 Seitenflächen fassen wir als Mantel zusammen:
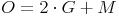
Grundfläche:
Bei einem vierseitigen Prisma handelt es sich bei der Grundfläche um ein Viereck. Da Grund- und Deckfläche kongruent sind, also um 2 gleich große Vierecke.
Mantel:
Schneidet man das vierseitige Prisma (ohne Grund- und Deckfläche) entlang einer senkrechten Kante auf und klappt die Seitenflächen um, so liegen nun alle 4 Rechtecke nebeneinander in einer Ebene.
Sie bilden zusammen ein großes Rechteck. Die Breite dieses großen Rechtecks entspricht der Höhe des Prismas, die Länge entspricht der Summe der 4 Seitenlängen der Grundfläche (= Umfang der Grundfläche):
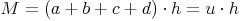
Grundfläche = Rechteck:
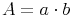
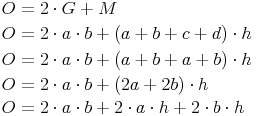
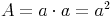
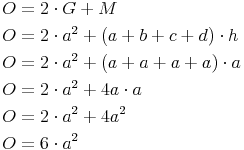
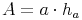
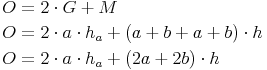
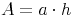
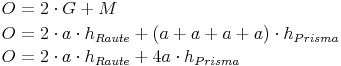
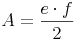
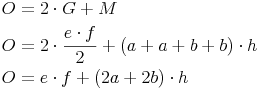
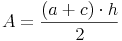
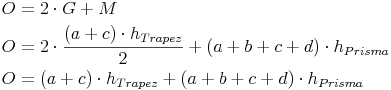
Oberfläche = 2 mal Grundfläche + Mantel
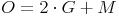
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Candy
Gute Zusammenfassung half meinem Bruder(4. Grundschule) sehr.
Alina
Mir hat es überhauptnicht geholfen! Ich wollte nach dem Oberflächeninhalt von einem Trapeznetz wissen und es ist zu dumm es mir rauszugeben... Sterne bewertung? 0,0 Sterne
Erich Hnilica, BEd
Liebe Alina!
Das ist das Kapitel "Vierseitiges Prisma". Zufällig wird hier auch die Formel zur Berechnung des Flächeninhalts eines Trapezes benötigt.
Wenn du mehr über die Flächeninhaltsformel des Trapezes wissen möchtest, dann musst du natürlich im entsprechenden Kapitel nachsehen:
Geometrie - Ebene Figuren - Vierecke - Trapez
Franz Huber
Ja Moin direkt angespickt von Arbeit und mitm Streber Arbeiten getauscht Jetzr habe isch ne 1, Exht Super