Raumdiagonale eines Quaders

Die Raumdiagonale(n) des Quaders

Eine Raumdiagonale verbindet jeden Eckpunkt der Grundfläche (A, B, C, D) mit dem am weitest entfernten (= gegenüberliegenden) Eckpunkt der Deckfläche (E, F, G, H):

$\overline{AG}\ , \overline{BH}\ , \overline{CE}\ , \overline{DF}$

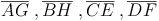
Die Seitenkanten des Quaders stehen normal auf die Grund- bzw. Deckfläche.

Somit ist jeder Punkt der Grundfläche gleich weit von der Deckfläche entfernt.

Aus diesem Grund sind die 4 Raumdiagonalen gleich lang.

Die Raumdiagonale eines Quaders wird daher einheitlich mit 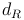bezeichnet.

Berechnung der Raumdiagonale eines Quaders

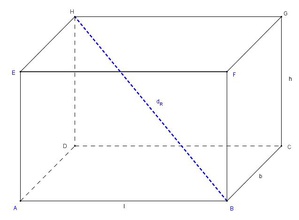
Zeichnet man eine beliebige Raumdiagonale des Quaders ein (z.B. jene vom Eckpunkt B zum Eckpunkt H), so entsteht ein rechtwinkeliges Dreieck (rechter Winkel im Eckpunkt D).

In jedem rechtwinkeligen Dreieck gilt der Lehrsatzes des Pythagoras, somit kann man mit dessen Hilfe die Länge der Raumdiagonale berechnen.

Die Raumdiagonale 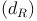(d_R) ist die Hypotenuse (=längste Seite) des rechtwinkeligen Dreiecks, die Höhe (h) sowie die Flächendiagonale der Grundfläche 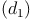(d_1) bilden die Katheten (= kürzeren Seiten). Daher gilt:

$\text{Hypotenuse} = \sqrt {\text{Kathete\ hoch\ 2} + \text{Kathete\ hoch\ 2}}$

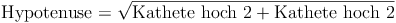
Wir setzen nun die Bezeichnungen in die Formel ein: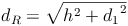
$d_R = \sqrt{h^2 + {d_1}^2}$

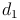Die Flächendiagonale kann folgendermaßen berechnet werden: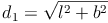
$d_1 = \sqrt{l^2 + b^2}$
${d_1}^2 = l^2 + b^2$

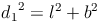
Für 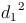${d_1}^2$ wird nun also l^2 + b^2 eingesetzt:
$d_R = \sqrt{h^2 + l^2 + b^2}$

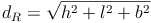
Nun kann noch die Reihenfolge der Summanden geändert werden: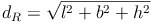
$d_R = \sqrt{l^2 + b^2 + h^2}$

Raumdiagonale eines Quaders:

In einem Quader sind alle Raumdiagonalen gleich lang und werden mit 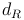bezeichnet.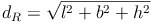

$d_R = \sqrt{l^2 + b^2 + h^2}$

Dieser Artikel hat mir geholfen. das half mir
... leider nicht ... leider nicht
Kommentar Kommentar
3,3
558 Bewertungen

Kommentar #41840 von Alperen 11.11.18 13:50 Alperen: Ich finde diese Seite super da es mir immer hilft die Aufgaben zu machen. VIELEN DANK!
Kommentar #44622 von dummheit 25.10.20 15:20 dummheit: ICH VERSTEHE ES NICHT DA IST KEIN RECHTWINKLIGES DREIECK!!!!!!!!
Kommentar #44812 von Apell 01.12.20 15:21 Apell: Wo ist die Herleitung? (vielleicht mal mit a b und c arbeiten)
Kommentar #48569 von JK 11.05.24 14:24 JK: Könntet ihr mir bitte sagen wo bei d1 ein rechterwinkel ist. Ohne ein rechten Winkel könnt ihr nicht den Satz des pythagoras anwenden.

Raumdiagonale eines Quaders

Die Raumdiagonale(n) des Quaders

Berechnung der Raumdiagonale eines Quaders

Kommentar verfassen

Ähnliche Arbeitsblätter